In structural engineering we give names to different structural members based on their behavior under applied load. If the primary mode of transfer of load is by bending then the structural member is termed as beam.
A beam is a structural element that is capable of withstanding load primarily by resisting against bending.
Beams generally carry vertical gravitational forces but can also be used to carry horizontal loads (e.g., loads due to an earthquake or wind). The loads carried by beams are transferred to columns, walls, or girders, which then transfer the force to adjacent structural members and finally to the ground.
Beams are characterized by their support condition, profile (shape of cross-section),geometry, equilibrium condition, and their material.
Classification based on supports
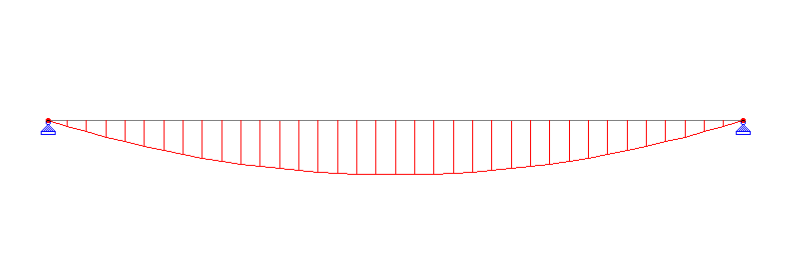
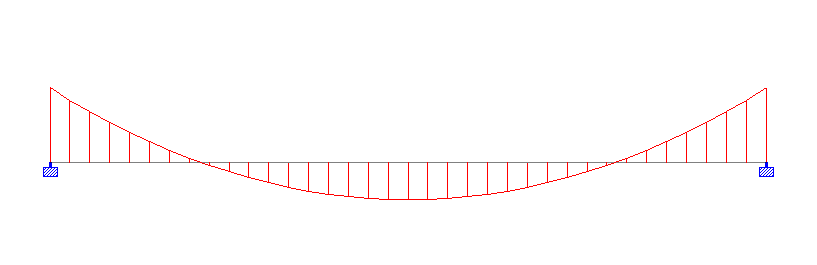
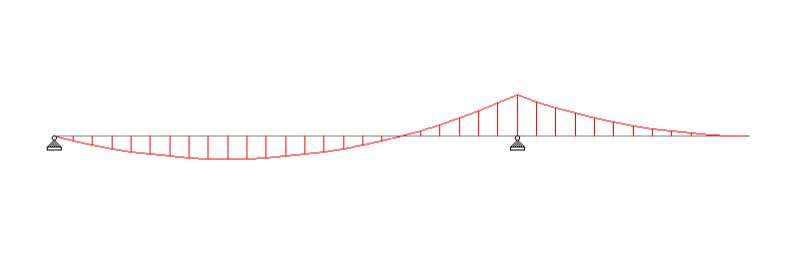
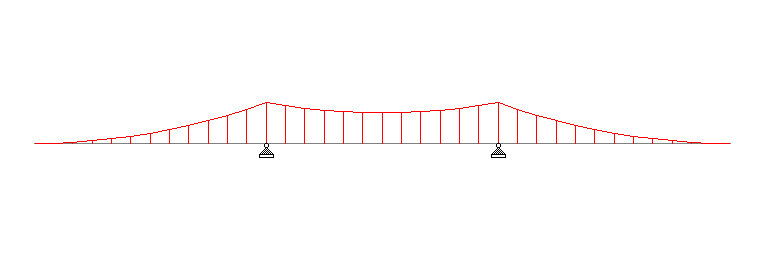
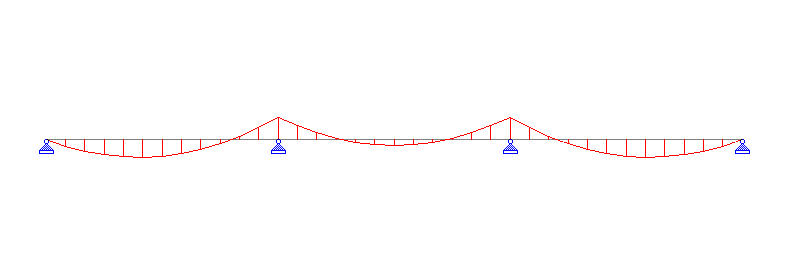
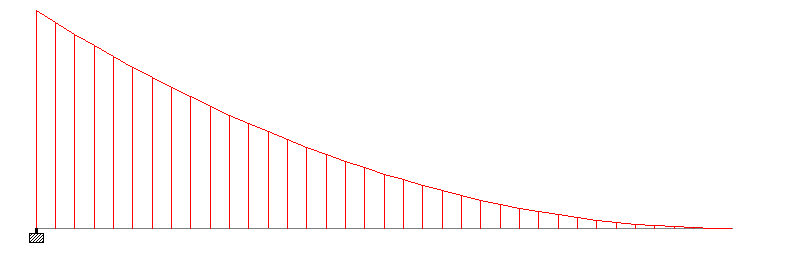
Classification of beams based on support condition is necessary because the bending moment acting on the beam is directly dependent on the support condition. You can see the variation in the following bending moment diagrams. For the same length and loading the bending moment diagram varies substantially with change in support condition.
- Simply supported – beams supported on the ends which are free to rotate and have no moment resistance.

- Fixed – beams supported on both ends and restrained from rotation.

- Over hanging – simple beams extending beyond its support on one end.

- Double overhanging – simple beams with both ends extending beyond its supports on both ends.

- Continuous – beams extending over more than two supports.

- Cantilever – a projecting beam fixed only at one end.

- Trussed – a beam strengthened by adding a cable or rod to form a truss.
Classification based on profile
The kind and magnitude of internal stress generated in the beam is directly dependent on the shape of the cross-section, thus requiring classification based on profile.
- Rectangular Beams
- I-Beams
- T-Beams
- C-Beams
- Other Cross-sections
Classification based on geometry
The kind and magnitude of internal stress generated in the beam is also directly dependent on the geometry of the beam, thus requiring classification based on geometry.
- Straight Beams
- Curved Beams
- Tapered Beams
Classification based on indeterminacy
Beam is primarily designed for bending moment and shear force. Evaluation of these bending moments and shear force is known as analysis. Based on the kind of analysis required to compute the reaction a beam is categorized into following two categories:
- Statically determinate beams: equilibrium conditions sufficient to compute reactions.e.g. simply supported beams, cantilever beams, single and double overhanging beams etc.
- Statically indeterminate beams: Deflections (Compatibility conditions) along with equilibrium equations should be used to find out reactions.e.g. propped cantilever, continuous beams, fixed beams.
Classification based on material
Different materials have different pros and cons for their use as a building material for the construction of beams in terms of cost and usability, thus beams are also characterized based on material used for their construction.
- Concrete Beams
- Steel Beams
- Timber Beams
Beam design
- RCC Beam Design is a free app for designing reinforced concrete beams as per Indian Standards.
- RCC Design and detailing could be performed by Limit State Method specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author