To understand equilibrium, let’s do some simple demonstrations. First, pick any bottle near you (mineral water bottle, cold drink bottle). Then, try to put it on the table in three different ways. You can see the figure to see the three different ways.
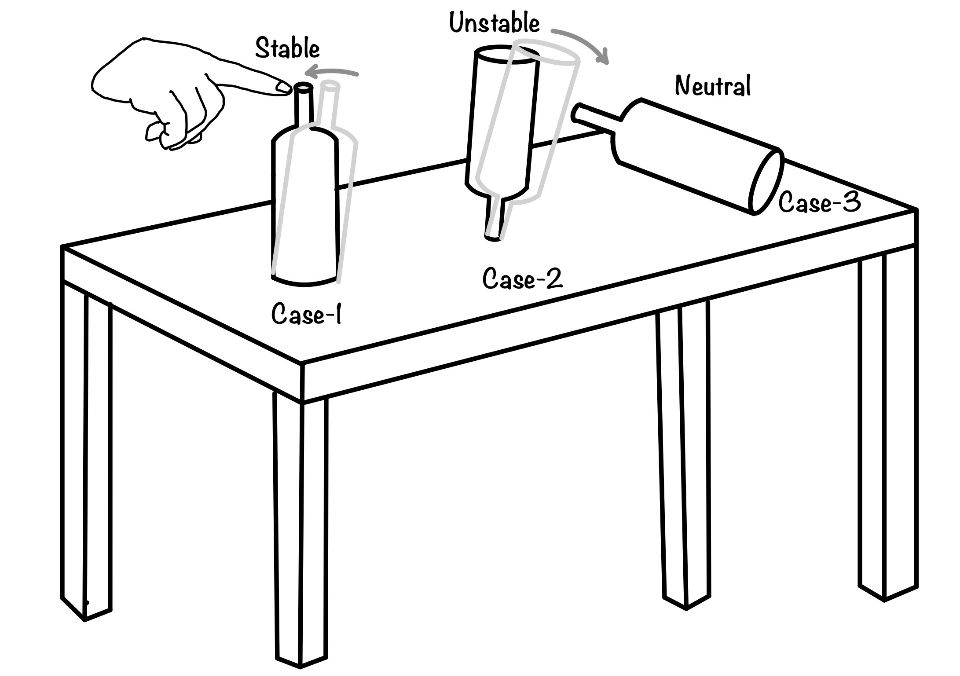
In the first case, it would have significantly less effort. You quickly and easily put the bottle from its base. The second method is also simple. But the third one is challenging.
Another observation is when you try to push the bottle slightly. The first one will come back in position, the second will topple, and the third will continue in motion.
In this post, you will learn about the definition of equilibrium, the equations of equilibrium in different dimensions, and the different types of equilibrium.
What is equilibrium?
The body is in equilibrium when any object’s linear and angular accelerations are zero. However, the accelerations are concerning to some inertial frames of reference.
What is static equilibrium?
You can consider that when both accelerations are zero, the body is at rest, and then the equilibrium in that stage is called the static equilibrium.
What is dynamic equilibrium?
That means when the accelerations are zero, they may have constant linear and angular velocities. Also, the object is in equilibrium and not in static condition. Then it is a dynamic equilibrium.
Are both of them the same?
But it all depends on the frame of reference. For example, the body is in motion with some frame of reference may be in the static condition in the other frame of reference.
Let’s understand this with the example, suppose you are traveling in the car. You have the object in front of you in the seat. Then the object is in static condition wi respect to you. But your friend outside the car finds the ball in motion.
Hence, the static and dynamic equilibrium is the same, and we may call it the equilibrium only.
What are the equations of static equilibrium?
If we want to write the equation in mathematical form, we can write for the translational equilibrium.
$$ \sum_i F_i = 0 $$
Where $F_i$ is the force in the body.
For rotational forces:
$$ \sum_i T_i =0 $$
Where, $T_i$ is the torque in the body due to applied forces.
What are the equations of equilibrium in 2d?
Now you want to find the reactions in the system by applying the equation. That means you want to apply the equilibrium in the two-dimensional.
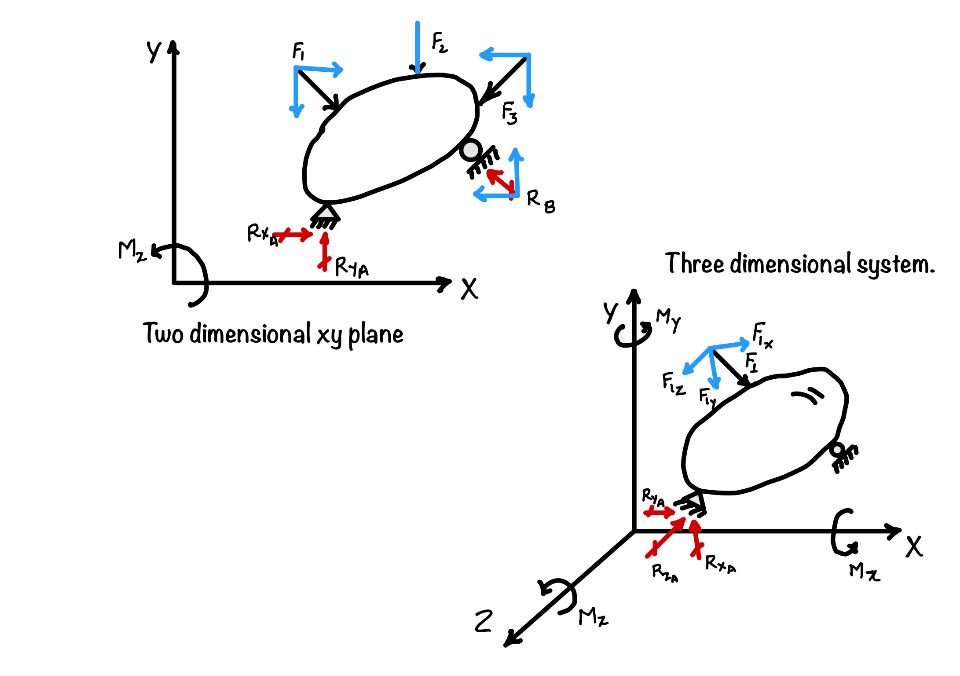
That means you want a simplified equation in the two-dimensional system, which you can use. Then the value of $i$ for two dimension system can be $x$ and $y$. This implies we can break all the forces in the $x$ and $y$ directions.
Hence we can write the equation as follows:
$$ \sum F_x =0 \\ \sum F_y = 0 $$
For the second equation of equilibrium:
Torque in $xy$ plane is a moment in $z$ direction. Hence, we can write it a
$$ \sum M_z = 0 $$
What are the equations of equilibrium in 3d?
What we did in two dimensions, we want to expand it to three dimensions. To do that, we need a three-dimensional coordinate system.
You can see in the figure that you have three translational forces and three moments in three dimensions. Hence writing the equation for three-dimensional coordinates:
Translational motion:
$$ \sum F_x = 0 \\ \sum F_y = 0\\ \sum F_z = 0 $$
For the rotational motion:
$$ \sum M_x = 0\\ \sum M_y = 0\\ \sum M_z = 0 $$
All these six equations are called equations.
What do we mean by stable and unstable equilibrium?
You must have performed the small demonstration at the beginning of the post. Now try to do the same from the top side of the bottle that you have observed.
The first case was straightforward, and even if you slightly deviated from the original position, it restored to its place. But in the second case, this was not true. It was challenging to keep the bottle straight. After lots of effort, if you could have done it, even slight touch may lead to the bottle toppling.
The first condition was the stable, and the third case was the unstable equilibrium.
Suppose you will try to lay down the bottle from the side, as shown in the second case of the figure. It’s easy to do that, but it will move when you apply force. And it will keep rolling until you stop it. In this case, you may call it neutral equilibrium.
Conclusion
Everybody wants to be in equilibrium. There are three types of equilibrium stable, unstable, and neutral. To find the reactions in any structural system, we need equilibrium equations. We need these equations to analyze the structures in two and three dimensions to draw SFD BMD.
In this post, you have learned the following key points:
- Equilibrium: When the translational and rotational acceleration of the body is equal to zero, then the body is in equilibrium.
- Stable equilibrium: When you disturb the body from its original position, it returns to its original position. The body is in stable equilibrium.
- Unstable Equilibrium: When a slight touch or force in the body causes large deformation, the body is in unstable equilibrium.
- Equation of equilibrium: When the body is in two dimensional $xy$ plane. The equation of equilibrium are $\sum F_x=0$, $\sum F_y =0$ and $\sum M_z =0$.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


