Euler’s critical load for fixed-free column

edited by Editorial Team |

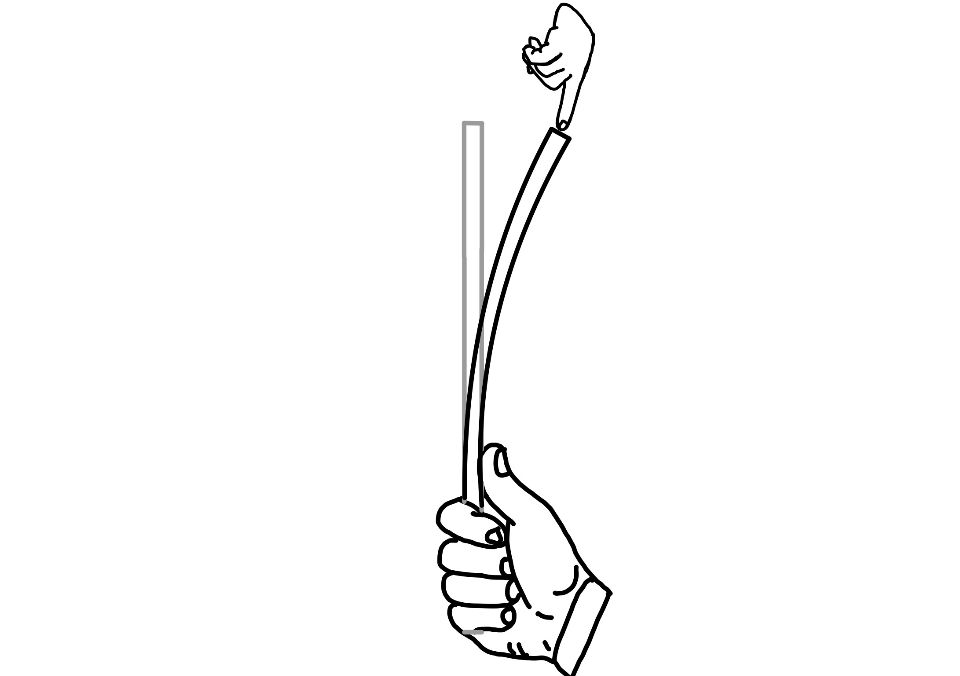
To understand this situation let’s try to hold the scale as given in the figure. This time hold the column from one end only. You may feel the difference in the column behavior. In this post we will find the critical load for the fixed-free column.

What are the assumptions in Euler’s critical load?

The Euler’s critical load is derived for the pinned condition, as we have derived in the previous article. We are again writing the assumption while deriving the critical load for other end conditions.

Euler’s critical load has the following assumptions:

  • The axis of the column is perfectly straight when unloaded.
  • The line of thrust co-insides with the unstrained axis of the column.
  • Flexural rigidity $EI$ is uniform.
  • Material is isotropic and homogenous.

What is differential equation for fixed-free condition

$$ -EI\frac{d^2y}{dx^2}=-{P(a-y)} \ EI\frac{d^2y}{dx^2}+Py= Pa $$

You can now write the solution for this differential equation

$$ y=C_1\sin{\sqrt{\frac{P}{EI}}}x+C_2\cos{\sqrt{\frac{P}{EI}}}x +a $$

What are the boundary condition for fixed-free conditions

$$ \text{ at }x=0 , y=0\ \text{ at } x=0 , \frac{dy}{dx}= 0 \ \text{ at } x= L, y=a $$

Based on these boundary conditions we can now find the values of constants.

This image shows the fixed-free end condition of the column. Another part shows the free body diagram of the column.

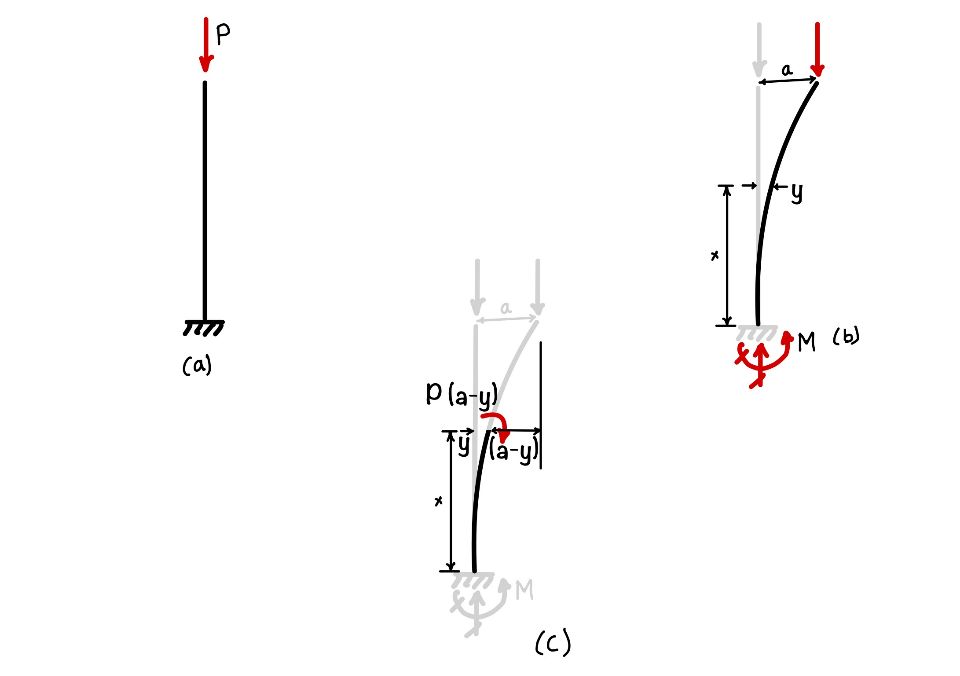
The solution equation is generated above when one end is fixed and the other free. Again repeating the same

$$ y=C_1\sin{\sqrt{\frac{P}{EI}}}x+C_2\cos{\sqrt{\frac{P}{EI}}}x +a $$

Now when we put $x=0$ in the above equation the first term $C_1\sin{\sqrt{\frac{P}{EI}}}x$ will be zero and the second term $C_2\cos{\sqrt{\frac{P}{EI}}}x$ will become $C_2$. Because the $\sin \theta =0 \text{ and } \cos \theta \text { at } \theta = 0$ . Hence we can calculate the value of $C_2$ as :

$$ \text{at } x=0 , y=0 \Rightarrow C_2 = -a $$

Now to apply the second boundary condition in the equation, we need to calculate the derivative of the equation.

$$ \frac{dy}{dx}=C_1\sqrt{\frac{P}{EI}}\cos{\sqrt{\frac{P}{EI}}}x-C_2\sqrt{\frac{P}{EI}}\sin{\sqrt{\frac{P}{EI}}}x $$

You can now put the boundary values in this equation. We will get

$$ \text{ at } x=0 , \frac{dy}{dx}= 0 \Rightarrow C_1 = 0 $$

Now after knowing the values of $C_1$ and $C_2$, we can substitute the values in the above equation.

$$ y=a\bigg( 1-\cos \sqrt{\frac{P}{EI}}x \bigg) $$

$$ \text{ at } x= L, y=a \Rightarrow a\bigg( 1-\cos \sqrt{\frac{P}{EI}}L \bigg)\\ \sqrt{\frac{P}{EI}}L = \frac{\pi}{2},\frac{3\pi}{2}, \frac{3\pi}{2} \dots $$

For the least significant value

$$ P_{cr}=\frac{\pi^2 EI}{4L^2} $$

Conclusion

In the series of these posts we have derived the critical load of the columns for different boundary conditions. In the present article we have discussed the different fixed-free end condition column.

You have learned following key concepts in this article:

  • Critical load: For the fixed-free column the critical load for buckling is $P_{cr}=\frac{\pi^2 EI}{4L^2} $.
  • Equivalent length: Equivalent length of the column having one end free and other fixed is $2L$.

Leave a Comment