Structures often experience significant temperature variations during their service life. These temperature changes can lead to the generation of stress within the structures. As engineers, it is our responsibility to calculate and understand the thermal loads on these structures to ensure their safety. Temperature variations can occur due to seasonal changes or daily fluctuations between day and night. In this article, we will explore temperature variations and the stress generated in structures as a result.
What is thermal thermal stress?
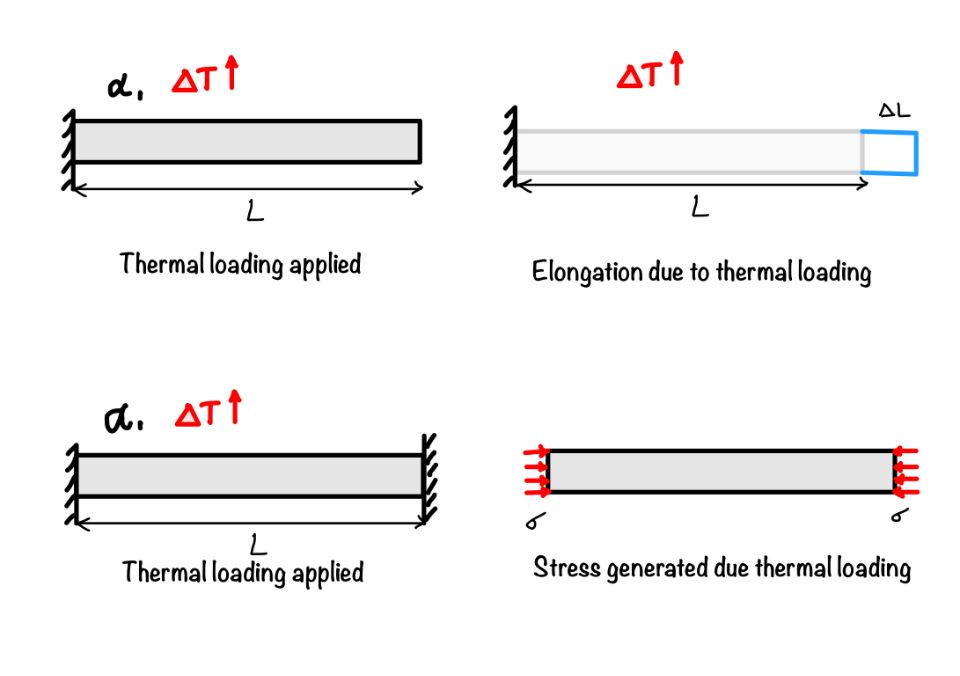
Thermal stress occurs when thermal loading induces stress in a structure. When temperature changes affect structures, they naturally undergo a change in length. You can calculate this change in length using the formula:
$$\Delta L = \alpha \Delta TL $$
Where:
- $\Delta L$ is the change in length,
- $\alpha$ is the thermal coefficient,
- $\Delta T$ is the change in temperature.
When we try to apply increase in temperature it causes elongation, while when we decrease the temperature this results in a shortening of the structure. Allowing this elongation to occur without restriction ensures that there is no stress in the structure. However, if we restrict or prevent this elongation, it may generate stress. You can observe this concept through a simple experiment by referring to the widget.
The stress produced in a member due to thermal changes can be calculated as follows:
$$\sigma = E \alpha \Delta T$$
Understanding the thermal stresses
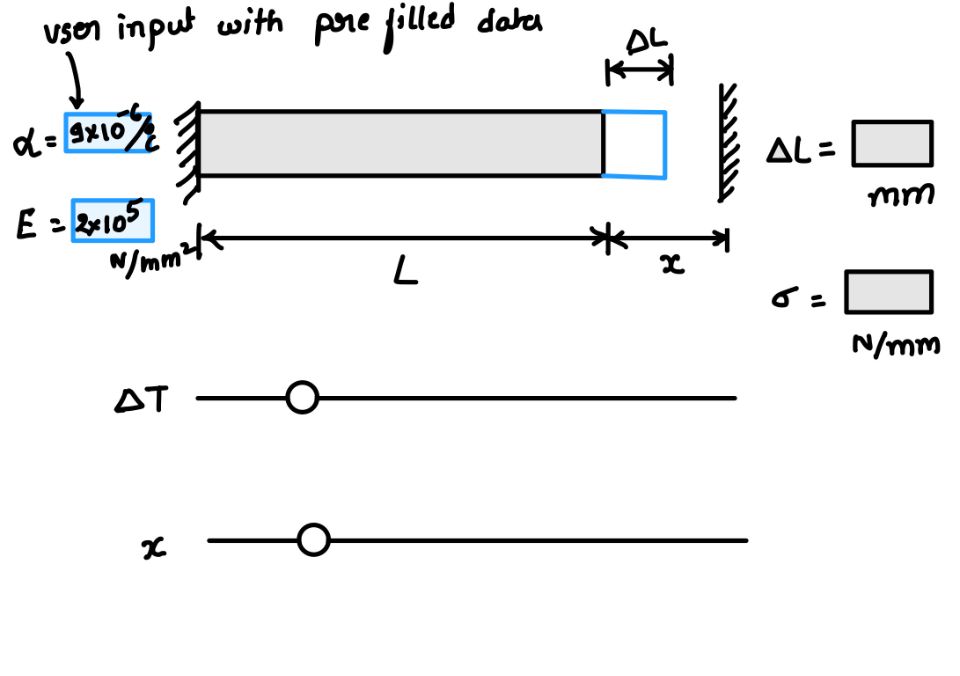
If you want to understand the thermal stress in the bar produced in the bar you can play with this widget. This bar is fixed at one end and other fixed end is at a distance $x$ from the other end.
So other end is fixed when $x$ is equal to zero. You can fix the value of $x$ to set the position of end condition. Now slide the point and increase the temperature of the bar. You will notice the elongation in the bar. The value of elongation showing in the box.
When the bar reaches the support, no elongation can occurs. After this the bar gains the stress. This stress is due to temperature increase and known as thermal stress. 
Limitations of thermal stress
Limitation of the formula discussed above:
- Linear behavior: The formula assumes linear behavior, which may not be valid for all materials and temperature ranges.
- Simple geometry: It does not account for complex material properties and geometry, which can affect stress distribution.
Application
Real-life applications of calculating thermal stresses include:
- Bridge Design: Engineers consider thermal stresses when designing bridges to accommodate temperature-induced expansions and contractions.
- Pipelines: In the oil and gas industry, pipelines must account for thermal stresses due to variations in fluid temperature.
Conclusion
Thermal stress is more important for space structures and structures that are subjected to more temperature variations.
In this blog, you have learned the following things:
- Understanding Thermal Stress: We learned that temperature changes in structures can cause thermal stress due to changes in length.
- Limitations: The formula we discussed has limitations, including linear behavior assumptions and neglecting material complexity.
- Applications: We explored practical applications of calculating thermal stresses in engineering.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


