This is the most important theorem in solid mechanics. To determine the deformation and the stress in the structure we can use the principle of minimum potential energy. A proper understanding of this theorem will make you strong in the structural domain. The principle of minimum potential energy is also useful in understanding the finite element concepts. The formal statement for the principle of minimum potential energy is as follows:
For conservative systems, of all the kinematically admissible deformations, those corresponding to the equilibrium state extrmize, the total potential energy. If the extremum is a minimum, the equilibrium state is stable.
If we consider a structural system as shown in the figure. This is a fixed structural system, pinned at the end. It will deform on the application of the force. From the original undeformed state, it will slowly move to a deformed state, and this is a deformation of the structural system. The deformation in the structure is the main unknown, as after knowing deformation we can calculate the strain from kinematic relation (strain-deformation relation). Strain will help in calculation the stress by using the consecutive relation (stress-strain relation) of the material.
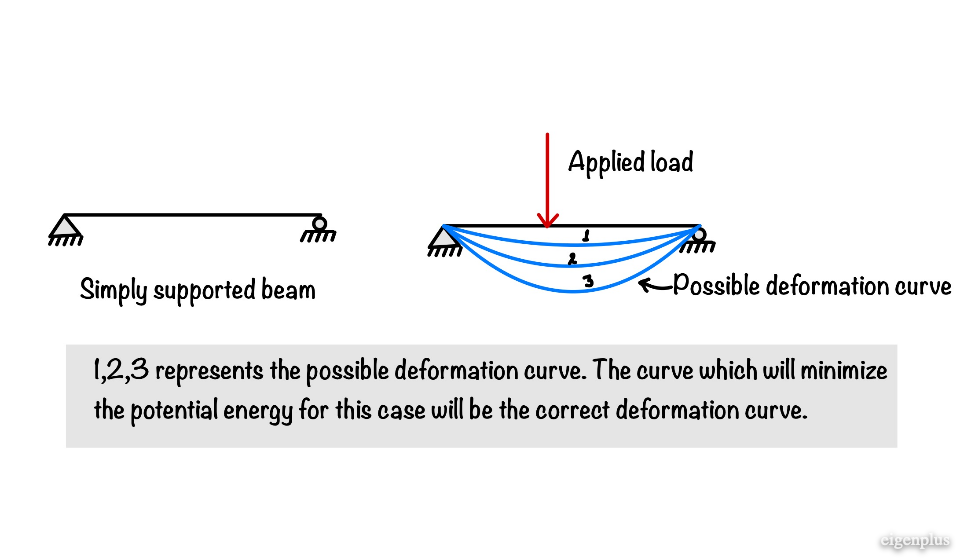
Therefore, the sole objective is to determine the deformation. Before proceeding further now we will define the potential energy first. So, The potential energy (PE) of a system is the sum of the strain energy(SE) and work potential(WP).
$$PE=SE+PE$$
Evaluation of potential energy
Now the question comes what is strain energy (SE) and how to find or calculate it, and the same question comes for the work potential (WP). When a structure will deform it will go under strain, and this deformed shape of the structure contains elastic energy that is known as strain energy. Hence, we have to integrate the strain energy density (strain energy per unit volume) over the entire volume of the structure which gives us the strain energy.
$$SE=\int_v{(\mathrm{strain\: energy\: density})dv}$$
where the strain energy density is :
$$ \mathrm{Strain\:energy\:density}=\frac{1}{2}(\sigma)(\epsilon)$$
Now, let’s talk about the work potential both structure. The work potential WP is the negative of the work done by the external force acting on the structure. And the work done by the external force is simply the force times the displacements at the points of application of forces as shown in figure.
Application of minimum potential energy principle
We are going to apply the minimum potential energy principle in the spring mass system. This example is just for your understanding of the principle. As shown in figure there is one spring, one end is fixed and other end is having one mass M. Our aim is to find the static equilibrium position of the mass after the application of force \(F\). We will solve this initially with force balance method, and later on compare this with the energy method.
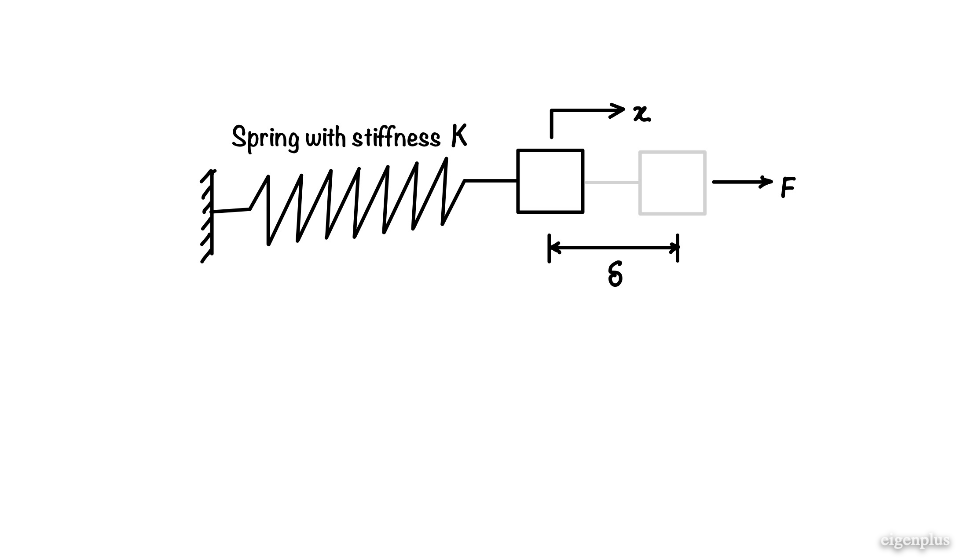
Spring will act when force starts moving the mass in the \(x\) direction. and the equilibrium position \(x_{equilibrium}\) will be at \(\delta=F/k\) as shown in figure.
We will perform the same calculations from the MPE principle instead of force-balance method. Now we will try to write the Potential Energy of the system first.
$$PE=SE+WP= \left(\frac{1}{2}kx^2\right)+(-Fx)=\frac{1}{2}kx^2-Fx$$
Now in the second step we have to find the value of \(x\) that will make the PE minimum. This value of \(x\) is the deformation for the problem. Hence, performing the differentiation of potential energy with respect to \(x\).
$$\frac{d(PE)}{dx}=0 \rightarrow kx-F=0 $$
$$ x_{equilibrium}=\delta=\frac{F}{k}$$
Further we can see that the second derivative of the potential energy is negative, hence the the extremum is minimum.
Also read: What is stress?

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


