When it comes to understanding how materials react under pressure, there’s a hidden superhero called Poisson’s Ratio. It’s a fascinating concept that sheds light on how things change shape when subjected to external forces. In this blog post, we’ll embark on a journey to demystify Poisson’s Ratio, exploring its significance and real-world applications.
The Shape-Shifting Scorecard
Imagine a piece of clay in your hand. When you press it down, it spreads outwards, becoming wider. Conversely, when you pull it upwards, it gets taller but also thinner from the sides. This inherent tendency of materials to change shape when compressed or stretched is beautifully encapsulated by Poisson’s Ratio.
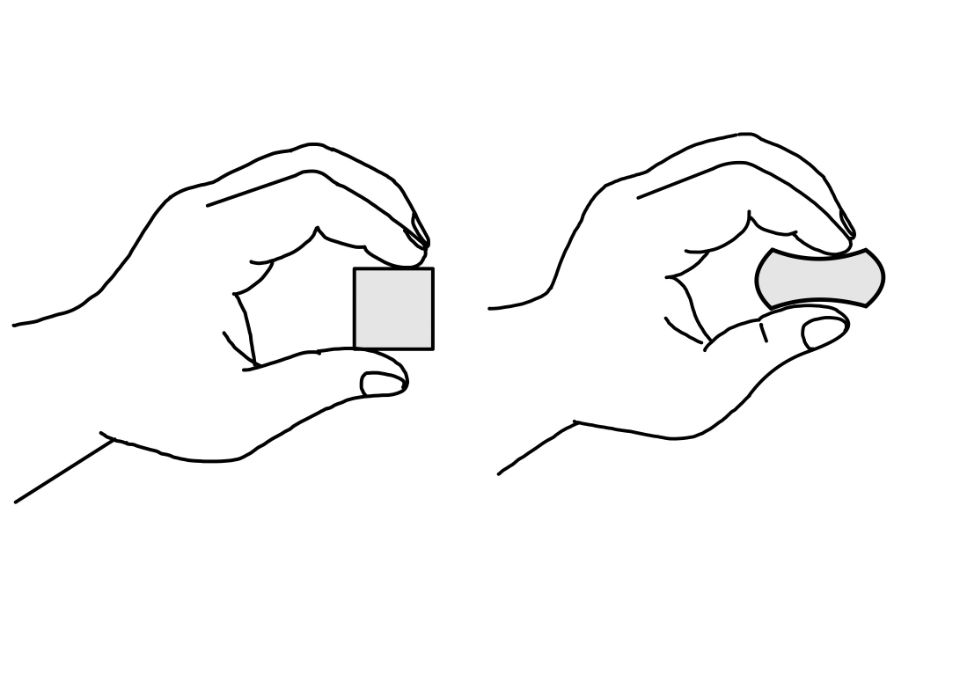
Definition: Poisson’s Ratio is a measure of how much a material tends to shrink in one direction when it is stretched or expanded in another. It’s like a material’s unique ‘shape-shifting scorecard’.
$$\nu = -\frac{\text{lateral strain}}{\text{longitudinal strain}}$$
Poisson’s Ratio in Action
To understand it in action, consider a rubber band. When you pull it lengthwise, the band gets thinner from the sides. This phenomenon exemplifies Poisson’s Ratio in a tangible way.
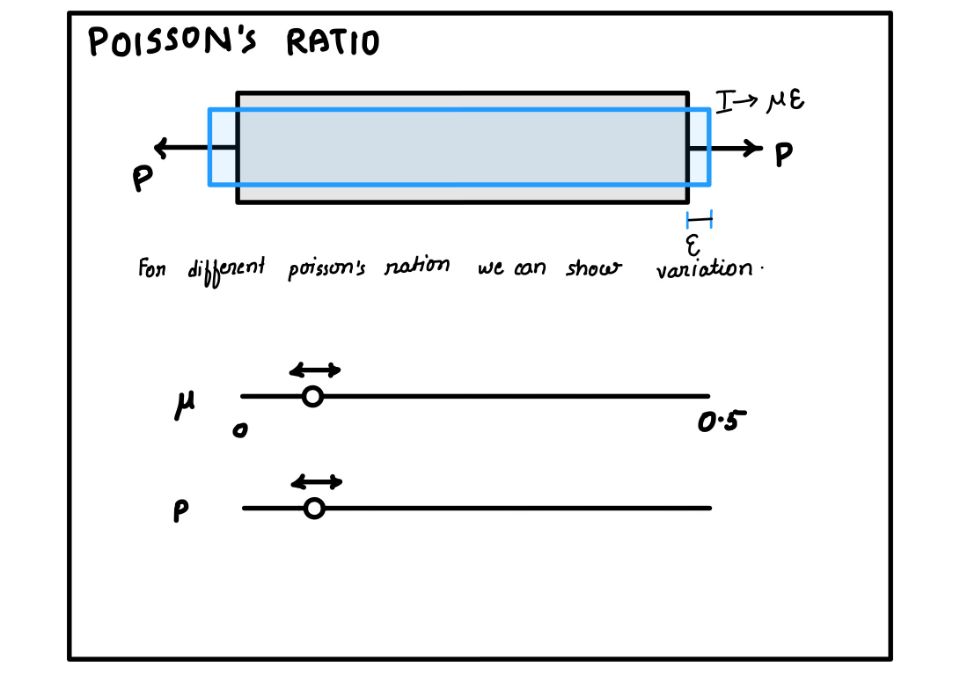
To understand this and have a feeling of it you can play with this. Try to make the material $\nu$ equal to zero and increase the pressure to see the change in the material and make it maximum and increase the load to see the change in the material.
The Magic Number: 0.5
Poisson’s Ratio is represented by the Greek letter ν (nu) and its value ranges between 0 and 0.5. For most common materials, the ratio hovers around 0.3 to 0.5. When it approaches 0.5, it implies that a material changes shape very easily. For cork, the Poisson’s ratio is 0.
Surprising Facts About Poisson’s Ratio
- Materials with a negative Poisson’s Ratio? Yes, they exist! These exotic materials actually expand in both directions when pulled. They’re like the ‘rebels’ of material science.
- Tailoring materials for specific applications: Engineers can select materials based on their Poisson’s Ratio. For instance, materials with a low ratio are suitable for applications where lateral expansion is undesirable.
When Poisson’s ratio is zero?
Believe it or not, there are instances where it reaches zero. This occurs in some highly specialized materials. When it is zero, it means that a material doesn’t change its width at all when stretched or compressed. It’s like a magical substance that refuses to budge, no matter the forces applied.
Materials with zero Poisson’s Ratio are rare and often have unique applications. They might be used in scenarios where lateral expansion or contraction is absolutely undesirable.
So, is a higher Poisson’s Ratio always better? Not necessarily! It all depends on the specific demands of the application and the behavior you want from the material.
Is a higher Poisson’s ratio better?
Now, you might be wondering, is a higher Poisson’s Ratio better? The answer depends on the context and the specific job a material needs to do.
A higher value means that a material is more inclined to change its shape when it encounters external forces. In certain scenarios, this can be a desirable trait. Imagine constructing a sturdy bridge or a towering skyscraper. You’d want the materials to adapt and distribute stresses evenly. In this case, a higher Poisson’s Ratio is like having a versatile performer in the cast, ensuring that the material can gracefully handle various types of stress.
Conclusion
In our journey to demystify Poisson’s Ratio, we’ve uncovered the remarkable role it plays in understanding how materials react under pressure. Just like a hidden superhero, this concept sheds light on the shape-shifting tendencies of materials when subjected to external forces. Here are some key takeaways to remember:
- Poisson’s Ratio Matters: It is not just a theoretical concept; it has real-world applications in engineering and material science. It helps engineers make informed choices when designing structures, ensuring that they can withstand the forces they’ll encounter.
- The Magic Number: It is represented by the Greek letter ν (nu), with values ranging from 0 to 0.5. Materials with higher ratios tend to change shape more readily, making them versatile for certain applications, while those with lower ratios are ideal when lateral expansion is undesirable.
- Materials with Unique Properties: Some materials exhibit negative or zero Poisson’s Ratios, offering distinctive characteristics that can be harnessed for specialized applications. Understanding these materials can open doors to innovative engineering solutions.
- Context Matters: Whether a higher or lower Poisson’s Ratio is better depends on the specific demands of the application. It’s all about choosing the right material for the job.
In the grand play of solid mechanics, Poisson’s Ratio takes center stage, reminding us that materials are dynamic performers in the ballet of engineering. So, the next time you encounter a rubber band, marvel at a skyscraper, or interact with everyday objects, remember that Poisson’s Ratio is at work, ensuring our world stays standing strong. It’s a lesson that highlights the interconnectedness of science, engineering, and our everyday lives, proving that even the most abstract concepts have a tangible impact on our world.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


