Definition of stress
Before defining stress at a point we must set the stage for the definition. Consider we have a deformable body, and this body bis in static equilibrium condition as shown in Fig (1). If the full body is equilibrium the part of the body will also be in equilibrium. Now we can define stress in this body. To maintain the equilibrium in the part of body and due to some deformation in the atomic level some internal forces are have to be there(as shown in Fig (3)).
Hence, Stress at a point is defined as “Intensity of internal force on the small area around the point of the deformable body.” The pictorial representation of this definition is shown in the figure below.
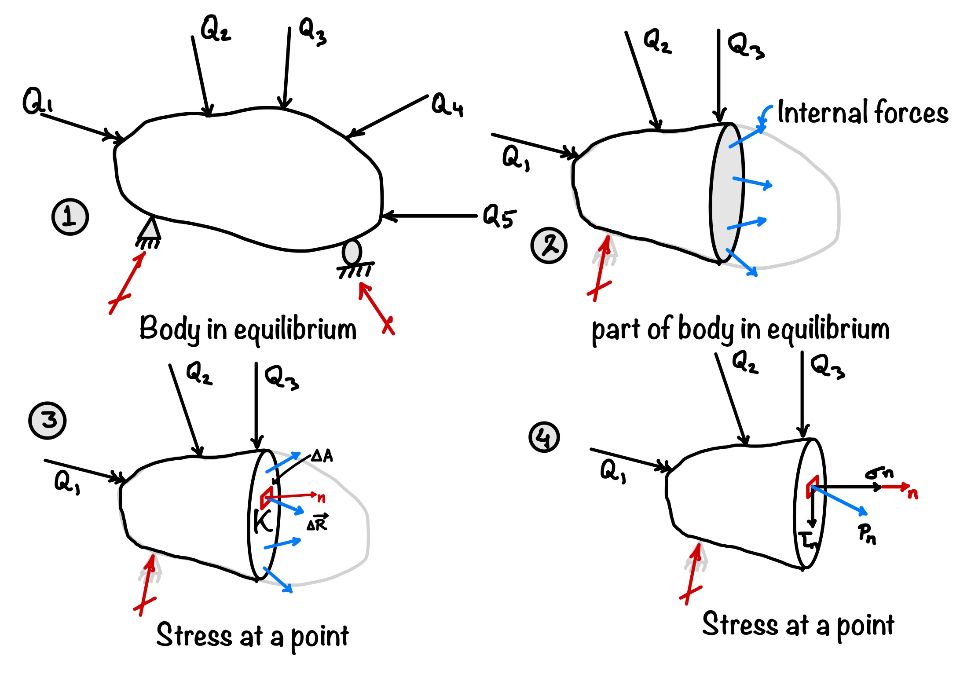
You can observe the above definition is at a point. It can be defined in the average sense as below:
$$\overrightarrow{ p}_{av}=\frac{\Delta R}{\Delta A}$$
As we have considered the body which is continuum in nature, hence, we can use the \(\Delta A \rightarrow 0 \). Then the stress on the area of normal \(n\) in vicinity of point \(K\) is
$$ \overrightarrow{p}_n= \frac{\Delta R}{\Delta A}$$ .
The unit is : SI system – \(Pascal\) Symbol \(Pa\) (\(N/m^2\))
So, after defining this we can see the dependency. As we can see from the figures these factors are position of point, magnitude and direction of the force and the orientation of the plane around the point affects the state-of-stress at any point. As, it is explained in the figure is inclined and have two component. One component is normal to area and other is tangential to the area. Normal component is Normal and tangential component is shear stress.
$$p_n=\sqrt{\sigma_n^2+\tau_n^2}$$
State of stress at a point
State of stress is summation of all stress at point on the all possible plane passing through the point. so, it is necessary to determine the strength of the material at that point. It is shown with the help of infinitesimal parallel-piped, in the vicinity of arbitrary chosen point of the body, as shown in fig.
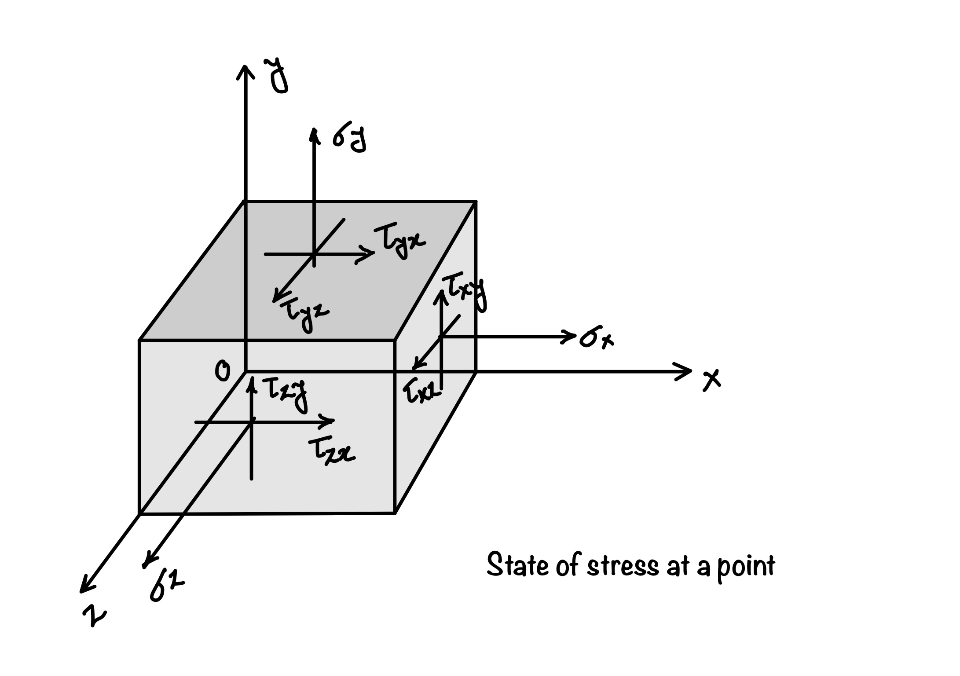
Assumption are the main building blocks in the mechanics of materials. These assumptions play very important role for the definition to be true. So in mechanics its very common practice that before defining any term we always have to discuss about the assumptions. With the change in the assumptions the definition also changes. So, lets discuss some assumptions for defining it.
Static equilibrium
Although you might be knowing the equilibrium. The first definition comes in your mind is summation of all the forces and moments in \(x,y,z\) direction are zero. That is very exact definition, and very good point to start with. Some points which we have to consider with this are:
- If a body is in equilibrium then all points inside the body are in equilibrium.
- Beam was in equilibrium when no load was there. Which is initial position. After application of load small deformation occurs and beam again comes in equilibrium called final position. These two position are same.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.