Beams, the backbone of any structural system, play a vital role in supporting loads and ensuring the stability of a building or structure. To ensure their safety, it is crucial to perform checks for shear , bond, and deflection. Let’s explore these checks and understand their practical application in beam design and analysis. By these checks effectively, engineers and designers can ensure the structural integrity and longevity of beams, thereby enhancing the overall safety of the built environment.
Firstly, shear bars are essential to enable beams to resist horizontal forces effectively. Shear bars, placed within the beam, enhance its capacity to withstand these forces and prevent shear failures.
Secondly, bond checks play a significant role in assessing the adequacy of the connection between concrete and steel. Ensuring a strong bond is crucial for stability and load transfer between the two materials, and ensures the overall strength of the beam.
Lastly, deflection checks are necessary to maintain the beam within the limits as per IS: 456: 2000. Managing this is vital to ensure optimal performance and prevent any potential failures due to bending or deformation.
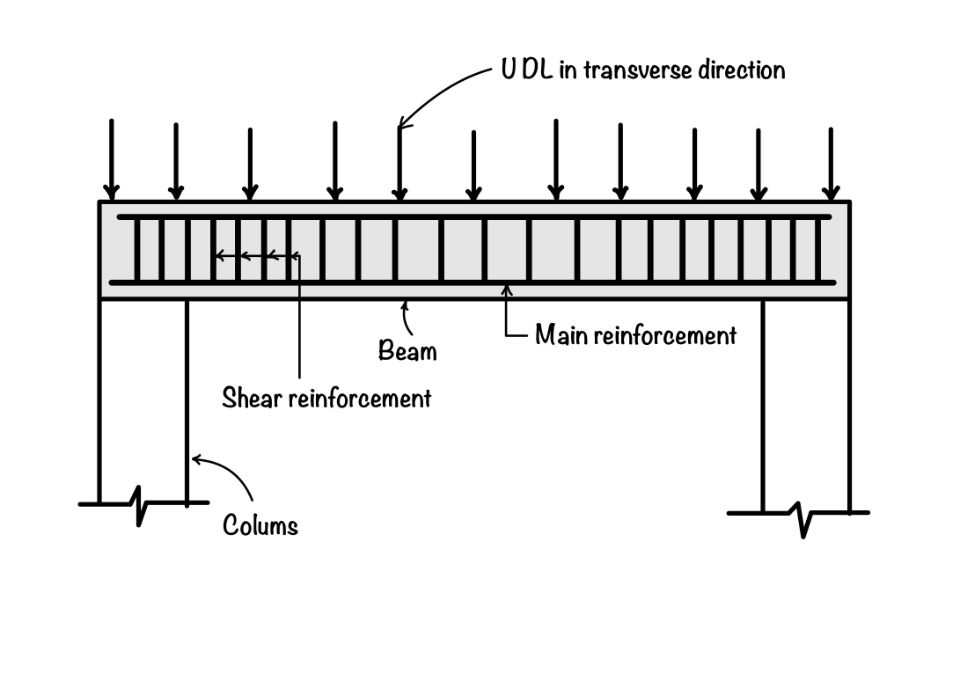
In this blog post, we will delve into the imp. of these checks and provide clarity into their practical application in the analysis and design of beams. By understanding these checks, engineers and designers can ensure the structural integrity and long life of beams, thus enhancing the overall safety of the built environment.
Check these post to know the initial analysis and design steps of the R.C.C beams, i.e., SRB and DRB.
1. Design of Shear Reinforcement
Firstly, shear bars strengthen the beam’s ability to resist horizontal forces, preventing shear failures. Additionally, they enhance the overall load-bearing capacity of the beam, enabling it to withstand heavy loads and external pressures. Moreover, shear bars effectively distribute the applied forces along the beam’s length, reducing concentrated stress points. In summary, shear bars are of utmost importance as they enhance the beam’s resistance to shear forces, increase its load- bearing capacity, distribute forces evenly, and improve its overall durability and resilience.
The step by step procedure to design of shear reinf. as per IS:456:2000 are as follows:
Calculation of total uniformly distributed load on beam
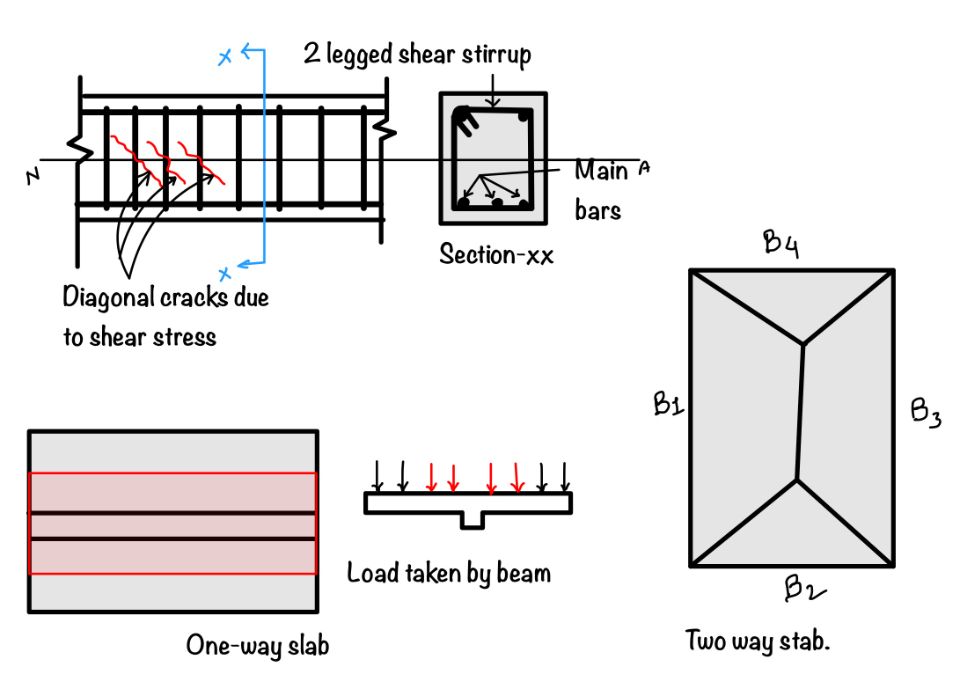
- For beam carrying one-way slab: The loads $w_u$ is the same as that calculated earlier for bending.
- For beam supporting two-way slabs: The load carrying is triangular/ trapezoidal loads, calculate equivalent uniformly distributed load for shear. For trapezoidal load, $$w_{u . e q s}=\frac{w_u L_x}{2}\left(1-\frac{1}{2 \beta}\right)=k_2 \times \frac{w_u L_x}{2}$$, where, $k_2=\left(1-\frac{1}{2 \beta}\right)$
- For triangular load on short edge beam carrying, two way slabs, $$w_{u . e q s}=w_u L_x / 4=k_2 w_u L_x / 2$$ where $k_2=1 / 2$ and for one way slab, $$w_{u . e q s}=w_u L_x / 6$$ where, $w_u=$ load on slab.
- Total load on beam $w_u = w_{u.eqs}$ from slabs on both sides + wall load + self weight
Calculate maximum shear $V_{ u.max }$ at the centre of support
$$ V_{u \cdot \max }=\alpha_d w_{u D} \times L+\alpha_L w_{u L} \times L $$
where, $\alpha_d$ and $\alpha_L=$ shear coefficients given in Table IS 456: 2000.
Check adequacy of concrete section
Compute maximum shear. resistance of conctete in diagonal compression.
$V_{w c \cdot \max }=\tau_{u c \cdot \max } b d>V_{u D}$ else revise the section by increasing $b$ or $D$, where $\tau_{uc}$ is the shear strength of concrete in diagonal compression.
Design shear, $V_{u D}=V_{u \max }-w_u\left(b_s / 2+d\right)$ for support offering compressive reaction.
$V_{u D}=V_{u \cdot \max }-w_u \times b_s / 2$ for support offering tensile reaction.
$b_s=$ Breadth of Support.
Determination of Necessity of Design of Shear Reinforcement
Compute shear resistance of concrete (V_{uc}) using the formula $V_{w c}=\tau_{u c} \cdot b d$., where the value of shear strength is decided as per Table of IS 456:2000 corresponding to percentage of tension steel at support and grade of concrete used.
Calculate the shear resistance of minimum stirrups ($V_{usv.min}$): Using the formula $V_{\text {usv.min }}=0.4 b d$.
Therefore, shear resistance of section with minimum stirrups ($V_{ ur.min }$): Using the formula $V_{u r \text { min }}=V_{u c}+V_{u s v \text { min }}=V_{u c}+0.4 b d$.
If $V_{u D}<V_{\text {ur.min }}$ provide minimum stirrups at spacing given by $$ s<\frac{0.87 f_y}{0.4 b} A_{s v} $$
Where, $A_{ sv }$ = total area of vertical legs of stirrups, b = width of the beam or breadth of web $b_w$, for flanged beams, and s ≤ (0.75d or 300 mm) whichever is less.
If $V_{u max}<V_{\text {ur.min }}$ it is even not necessary to calculate $V_{uD}$ but only minimum stirrups are required to be provided.
If $V_{u D}<V_{\text {ur.min }}$, design the shear reinforcement.
Shear Reinforcement
Shear carried by shear bars = $V_{us} = V_{uD} – V_{uc}$
If bent up bars are used, calculate shear carried by bent up bars
$$ V_{u s b}=0.87 f_y A_{s b} \sin \alpha \ngtr 0.5 V_{u s} $$ where, $A_{s b}=$ area of bent up bar $\alpha=$ angle between bent up bar and beam axis $=0.707 $ for $\alpha=45^{\circ}$
Bend the bar at a distance of $1.5 d(>2 d)$ from the centre of support. If bent up bars are not provided, $V_{ usb} = 0$
Ultimate shear to be carried by stirrups, $V_{u s v}=\left(V_{u s}-V_{u s b}\right) \notin 0.5 V_{u s}$ or $V_{u s v}=V_{u s}$ when bent up bars are not provided.
Spacing $s$ of design stirrups of area $A_{ sv }$ is given by:
$$ s=\frac{0.87 f_y A_{s v} d}{V_{u s v}} $$ $s \leqslant(0.75 d$ or $300 \mathrm{~mm})$ whichever is less.
Calculate the zones of shear reinforcement (When $V_{ usb } = 0$
- Zone – I : Zone of design shear reinf. $\quad L_{s l}=\left(V_{u \cdot \max }-V_{u r \cdot \min }\right) / w_u$
- Zone – II : Zone of minimum shear bars $L_{s 2}=\left(V_{u r \text { min }}-0.5 V_{u c}\right) / w_u$ If $V_{u \cdot \max }<V_{u r \text { min }}$ or $V_{u D}<V_{u r \text { min’}} \quad L_{s l}=0, L_{s 2}=\left(V_{u \cdot \max }-0.5 V_{u c}\right) / w_u$
- Zone – III : Zone of nominal shear reinforcement $L_{s 3}=0.5 V_{u c} / w_u$
In zone $L_{ s3 }$, minimum dia. of stirrup of 6nm at maximum spacing $\ngtr(0.75 d$ or $300 \mathrm{~mm})$ should be provided.
2. Check for Bond
Bond is not very critical in beams. If necessary check for development length may be satisfactory at simple support and at point of contraflexure. Firstly, this check ensures that the connection between the two materials is strong enough to handle the loads placed on the beam. It helps us identify any weak spots or problems in the bond so that we can reinforce or fix them. A good bond check also ensures that the load transfer between the concrete and steel is smooth, without any slipping or detachment. By carefully checking the bond, we can make sure that the beam is stable and reliable, which is crucial for the overall safety and durability of the structure.
3. Check for Deflection
Checking for deflection in beams is vital for ensuring their optimal performance and preventing structural failures. Firstly, it allows us to monitor and manage the amount of bending or deformation that occurs when the beam is under load. By doing so, we can ensure that the deflection remains within acceptable limits, avoiding excessive sagging or bending that could compromise the beam’s stability.
Additionally, a thorough deflection check helps us identify any potential weaknesses or areas of concern, allowing us to take necessary measures to reinforce or adjust the beam design if needed. Furthermore, by controlling deflection, we can ensure that the beam effectively supports the intended loads and maintains its shape and structural integrity over time.
Check that $d_{ prov. } > \frac{L}{L/D \alpha_1 \alpha_2 \alpha_3 \alpha_4}$
In the case of beam this criteria is normally satisfied, because L/d < 16 and hence computations are skipped.
If necessary, calculate the actual deflection and check with permissible value. Regular deflection checks provide valuable insights into the performance of the beam and enable us to address any issues promptly, enhancing the overall safety and reliability of the structure.
Conclusions
The incorporation of thorough checks for shear reinforcement, bond, and deflection is paramount in ensuring the structural integrity and safety of beams.
The key takeaways are as follows:
- Shear reinforcement: It strengthens the beam’s ability to resist horizontal forces, preventing shear failures.
- Ensuring Structural Integrity: Thorough checks for shear reinforcement, bond, and deflection are essential for ensuring the structural integrity and safety of beams.
- Essential Checks for Shear Reinforcement: This enhances the beam’s ability to resist horizontal forces and prevents shear failures.
- Essential Checks for Bond: Bond checks assess the bond strength between concrete and reinforcing steel, ensuring stability and load transfer.
- Deflection in Beams: Managing deflection within acceptable limits ensures optimal beam performance and prevents structural failures.
Overall, these checks for shear, bond, and deflection ensure the integrity and safety of beams. Shear reinforcement prevents shear failures, and essential checks for bond guarantee stability and load transfer. Managing deflection within acceptable limits maintains optimal beam performance and prevents structural failures.
Beam design
- RCC Beam Design is a free app for designing reinforced concrete beams as per Indian Standards.
- RCC Design and detailing could be performed by Limit State Method specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


