You must be knowing different elastic constants, like the modulus of elasticity, rigidity, bulk modulus, and Poisson’s ratio. These are different elastic moduli having different meanings. But all these elastic constants are only partially independent of each other. Surprised! Don’t be. Yes, you can calculate the one from the others. In this post, we will take you to the basic meaning of elastic constants and briefly explain the definition of different constants. And yes, we will also prove the relationship between them.
Definition of different elastic constants
Before understanding the relation between them, you must know how to define them. In this section, we will explain the elastic constants.
All these definitions are for the homogeneous and isotropic and homogeneous material.
- Modulus of Elasticity: When the material is under a proportional limit, stress is directly proportional to strain. This is denoted by the \(E\), and
$$ E=\frac{\sigma}{\varepsilon} $$
- Modulus of rigidity: When the material is subjected to shear, the elastic modulus for shear is known as the modulus of rigidity. $$ G=\frac{\tau}{\gamma} $$
- Bulk modulus: It is the ratio of volumetric stress to volumetric strain. $$ K=\frac{\sigma_v}{\frac{\Delta V}{V}} $$
- Poisson’s ratio: The strain developed in the lateral direction due to longitudinal stress is due to Poisson’s effect. The ratio of lateral strain to longitudinal strain.
$$ \nu=\frac{- \varepsilon_{lateral}}{\varepsilon_l} $$
What is the elation between the G and E
Application of shear force in cuboid
The modulus of rigidity is connected with the modulus of elasticity. As shown in the figure, you need to apply the shear in the block \(ABCD\). This shear will create deformation, and the distorted shape is \(ABC’D’\).
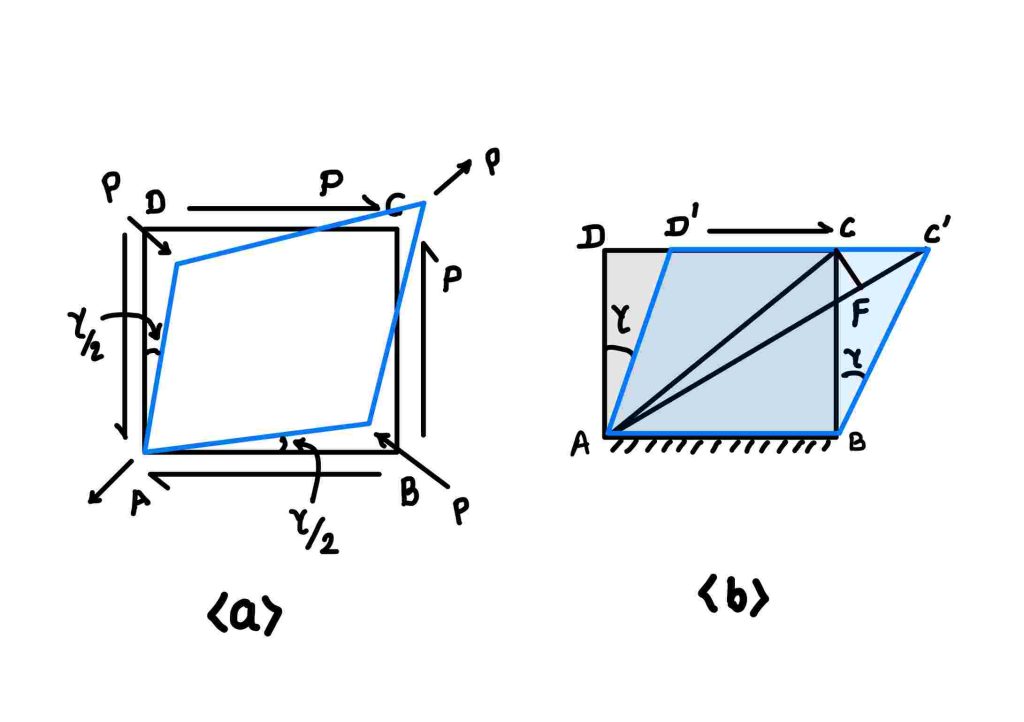
Computation of strain in diagonal AC
The shear strain for this case is \(\gamma=\frac{CC’}{BC}\). Not to connect this with the elastic constant, you need to define the strain of line AC. Which is :
$$ \varepsilon_{AC}=\frac{FC’}{AC} $$
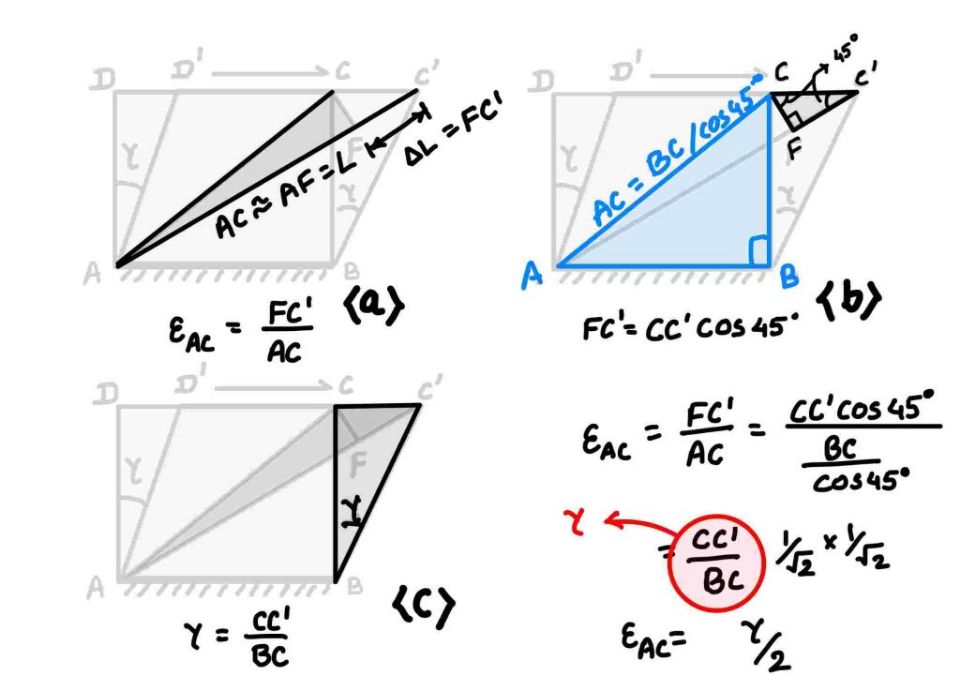
Now from the figure. Consider the triangle \(\Delta CFC’\) , in this \(FC’=CC’\cos (45)\). Again, consider the triangle \(\Delta ABC\), in this \(AC\cos(45)=BC\). Now you know what we have to do. You are right; we must substitute these values in the \(\varepsilon_{AC}\).
$$ \varepsilon_{AC}=\frac{FC’}{AC}=\frac{CC’\cos(45)}{\frac{BC}{\cos(45)}}=\frac{CC’}{2BC}=\frac{\gamma}{2}=\frac{\tau}{2G} $$
Now next step will be to define the strain of this line using elastic modulus \(E\). How can you achieve this target? Take some pause and start thinking. This will develop a critical thinking attitude in you. And you don’t have to memorize the step.
Calculation of force in diagonal direction
I hope you have a rough idea, and now it’s time to check it. Yes, you are right; we have to think about the extension of line \(AC\); hence we need the stress value in its longitudinal direction. Now, following your suggestions. Draw the block \(ABCD\) again to evaluate the stress in the diagonal direction. The force balance equation in the axial direction of the line $AC$ and in the transverse direction of the line \(AC\).
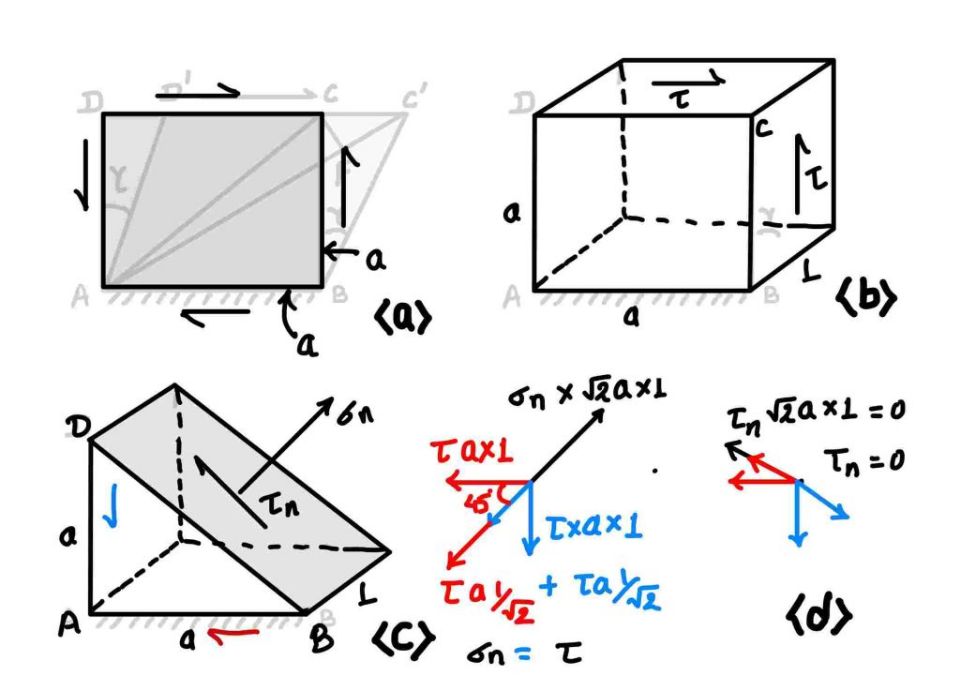
From the figure, you can conclude that the stress in the axial direction is \(\tau\) and the stress in the transverse direction is \(-\tau\). We know you can easily calculate the strain of line \(AC\) for this stress condition.
$$ \varepsilon_{AC}=\frac{\tau}{E}-\nu \frac{-\tau}{E}= \frac{\tau}{E}(1+\nu) $$
After this, you know the mathematics and know what to do. You have to equate both strains of line \(AC\).
$$ \frac{\tau}{2G}=\frac{\tau}{E}(1+\nu) \rightarrow E=2G(1+\nu) $$
This is the relation between the material’s \(E\) and \(G\). But always remember the material must be homogeneous and isotropic and follows Hooke’s law.
What is the elation between K and E?
To define the relation between the bulk modulus and elasticity, we need to define the volume change of the cube. Hence consider one cuboid for understanding, with dimensions \(a,b,c\) as shown in the figure. Now apply the stress in all three dimensions. These stresses will produce strain in all three directions. These strains will change the volume of the cube.
Volume of the cuboid
$$ V=abc $$
Change in length or strain in the $x$ direction will be the direct strain due to \(\sigma_x\) and the lateral strain in $x$ due to applied stresses \(\sigma_y, \sigma_z\) will be \(-\nu\frac{\sigma_y}{E}, -\nu\frac{\sigma_z}{E}\).
$$ \varepsilon_x=\frac{\sigma_x}{E}-\nu\frac{\sigma_y}{E}-\nu\frac{\sigma_z}{E} $$
Similarly for $y$ and $z$ axis you can obtain,
$$ \varepsilon_y=\frac{\sigma_y}{E}-\nu\frac{\sigma_x}{E}-\nu\frac{\sigma_z}{E}\\\varepsilon_z=\frac{\sigma_z}{E}-\nu\frac{\sigma_y}{E}-\nu\frac{\sigma_x}{E} $$
Due to strain, the new dimension of the cuboid will be as follows
$$ a\rightarrow a+a\varepsilon_x\\ b\rightarrow b+b \varepsilon_y\\ c\rightarrow c+c \varepsilon_z $$
with this new dimension, we will find out the new volume
$$ V=abc(1+\varepsilon_x)(1+\varepsilon_y)(1+\varepsilon_z)\\V=abc(1+\varepsilon_x+\varepsilon_y+\varepsilon_z+\varepsilon_x\varepsilon_y+\varepsilon_y\varepsilon_z+\varepsilon_z\varepsilon_x+\varepsilon_x\varepsilon_y\varepsilon_z) $$
The numerical value of strain is very less, and you know when we multiply the two such numbers, it will become lesser, and because of this reason, we omit these terms from the calculation. Neglect the higher order terms from the above expression we get.
$$ V=abc(1+\varepsilon_x+\varepsilon_y+\varepsilon_z) $$
With this expression, you can easily extract the change in volume \(\Delta V\).
$$ V=V_0+\Delta V\\V=abc+abc(\varepsilon_x+\varepsilon_y+\varepsilon_z)\\\Delta V=abc(\varepsilon_x+\varepsilon_y+\varepsilon_z) $$
Substituting the strain values from the above expressions. we will get this in the following form
$$ \Delta V= V_0\frac{1}{E}[(\sigma_x-\nu\sigma_y-\nu\sigma_z)+(\sigma_y-\nu\sigma_x-\nu\sigma_z)+(\sigma_z-\nu\sigma_x-\nu\sigma_y)]\\\Delta V=V_0\frac{1}{E}[(1-2\nu)(\sigma_x+\sigma_y+\sigma_z)] $$
If we apply the equal stress in all directions, it will become volumetric stress, and \((\sigma_x+\sigma_y+\sigma_z)\) becomes equal to \(3\sigma\). From the definition of bulk modulus, we know $K$. replacing the \(K\) in the above expression
$$ \frac{\frac{\Delta V}{V_0}}{(3\sigma)}=\frac{1}{E}(1-2\nu)\\\frac{1}{3K}=\frac{1}{E}(1-2\nu)\\E=3K(1-2\nu) $$
? Remembering the elastic relation between the modulus of elasticity and bulk modulus helps fast solving.
Relation between elastic constants in a nutshell
Many assumptions and calculations are involved while developing the relation between the elastic constants. However, this assumption makes the problem simple.
In this post you have learned following key concepts:
- Elasticity and modulus of rigidity: The relation between the modulus of elasticity and modulus of rigidity is $$E=2G(1+\nu)$$
- Elasticity and bulk modulus: The relation between the modulus of elasticity and bulk modulus is $$E=3K(1-2\nu)$$
- Independent constants: When you can derive one constant from another, they are independent elastic constants. Hence, the number of independent elastic constants for the homogeneous and isotropic material is 2.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author



E = 3K (1- 2v).. please check it
Thank you Abhinand,
For pointing out the typo and reading the full article carefully. Please write to us, if you want detailed article on some specific topic.