While reading the strength of the material, we come across different moduli. One of these moduli is the modulus of rigidity. In this article, we will see the definition of rigidity, its use, and its existence in the constitutive equation for isotropic, linear elastic, and homogenous material.
What is the modulus of rigidity?
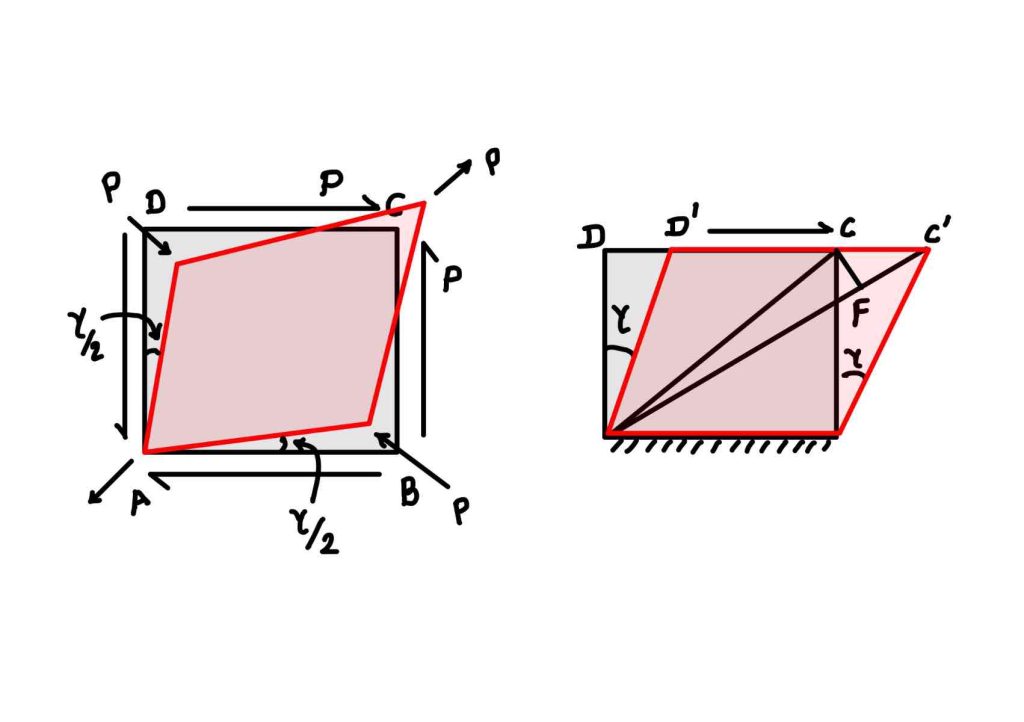
You are familiar with modulus of elasticity. When you apply modulus of elasticity in shear it is modulus of shear. We represent this by $G$. It is the ratio of shear stress to shear strain. It has the same dimension as shear stress ($N/mm^2$) as the shear strain is dimension less quantity.
$$ G=\frac{\tau}{\gamma} $$
Where $\tau$ is the shear stress acting in the materia., and $\gamma$ is the shear strain which we measure in the direction of shear stress application.
Where do we use modulus of rigidity?
The rigidity basically shows the resistance to torsion in the shaft or beam. So when we design the beam, the torsion in the beam is responsibility of rigidity.
How this reflects in the constitutive relation?
For isotropic, linear elastic, and homogenous material this can be calculated from the other elastic constants.
$$ G=\frac{E}{2(1+\nu)} $$
Where $E$ is the modulus of elasticity, $\nu$ is the Poisson’s ratio.
Conclusion
With this post, you have learned:
- Definition: The modulus of elasticity in shear is known as the modulus of rigidity.
- Relevance: The modulus of rigidity shows the beam’s torsion capacity; the more rigidity, the more the torsion carrying capacity.
- Existence: This is not an independent elastic coefficient for isotropic, linear elastic and homogenous material.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.