Before discussing seepage here in this article we have already discussed about seepage in Permeability of soil and its measurement and also in seepage force. But the difference between the topics is the dimension. In the earlier topics we have discussed about the one dimensional flow of water through the cross section of soil. But in this topic we will discuss about the two dimensional flow of water and seepage force generated due to this flow. One dimensional flow is ideal situation. But in practical situation like sheet pile wall, earthen dam cross section and many more flow occurs in two dimensional.
Two dimensional flow
As we can see in the Fig below, first case is one dimensional flow. Direction of flow of water is perpendicular to cross section. Flow of water is not changing the direction. This is very simple phenomenon. Here by knowing coefficient of permeability we can easily calculate the seepage force. But as shown in the second part of the fig. Two dimensional flow is shown. Here the velocity and direction of flow is changing from point to point.
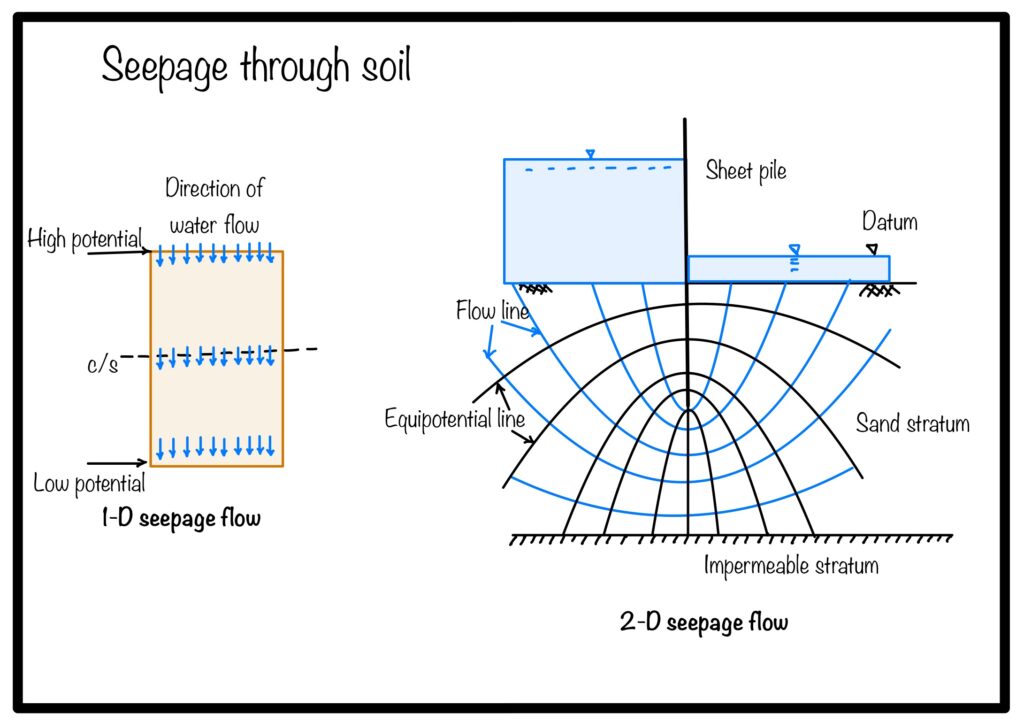
Assumption in seepage flow
There are few assumption which make the analysis easy. These assumptions are as follows:
- Soil medium is fully saturated, so that Darcy’s law could be valid.
- Soil mass is homogeneous and isotropic, only for the derivation of Laplace’s law. After deriving it we could extend it this to anisotrpic previous medium.
- Fluid and soil both are in-compressible.
- Flow condition don’t changes with time, hence steady state condition exists.
Lapalce Law
Consider an soil element with size \(dx\) and \(dz\) in \(x\) and \(z\) direction respectively. Flow with velocity \(V_x\) and \(V_z\) in (x) and (z) direction respectively. After traveling a distance \(dx\) flow velocity \(V_x\) changes to \(V_x+\frac{\partial {V_x}}{\partial{x}}dx\) and similar phenomenon happens in \(z\) direction also.
After the flow basic conservation principle could be applied that is
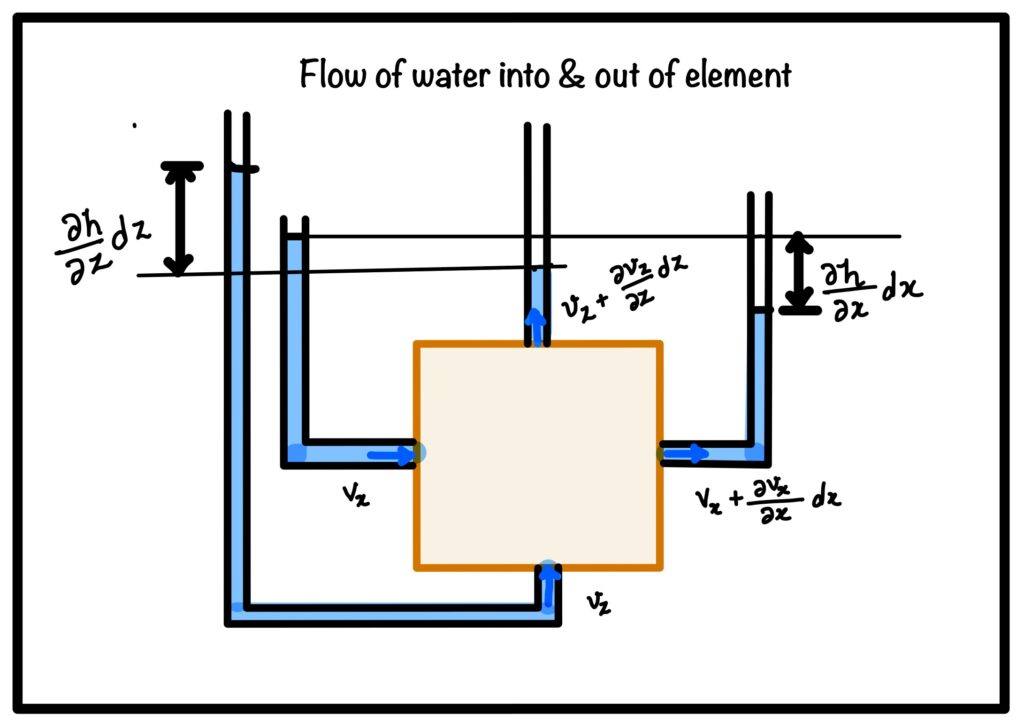
Amount of water going in is equal to amount of water going out.
$$ V_x dydz+V_z dxdy = V_xdydz+\frac{\partial {V_x}}{\partial{x}}dxdydz +V_zdxdy+\frac{\partial {V_z}}{\partial{z}}dxdydz$$
$$\frac{\partial {V_x}}{\partial{x}}+\frac{\partial {V_z}}{\partial{z}}=0$$
Now assuming the validity of Darcy’s law:
$$V_x=k_xi_x=k_x\frac{\partial{h}}{\partial{x}}; V_z=k_zi_z=k_x\frac{\partial{h}}{\partial{x}}$$
Again assuming the soil is homogeneous. (by assuming homogeneous we make sure that \(k_x\) & \(k_z\) are same at every point in the domain)
$$\frac{\partial{V_x}}{\partial{x}}=k_x\frac{\partial^2{h}}{\partial{x}^2}; \frac{\partial{V_z}}{\partial{z}}=k_z\frac{\partial^2{h}}{\partial{z}^2}$$
and if the soil is isotropic also. That means coefficient of permeability in both direction will be same. Hence, above equation will become
$$\frac{\partial^2{h}}{\partial{x}^2}+\frac{\partial^2{h}}{\partial{z}^2}=0$$
This is Lapace’s equation. Solution of the above equation will be set of orthogonal curves. These curves are
- Flow lines
- Equipotential lines

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.