Put the paper on the table and try to push the paper from both sides. What will you find? You will find that when you push the paper, the mid portion of the paper rises from the table. This phenomenon is called buckling.
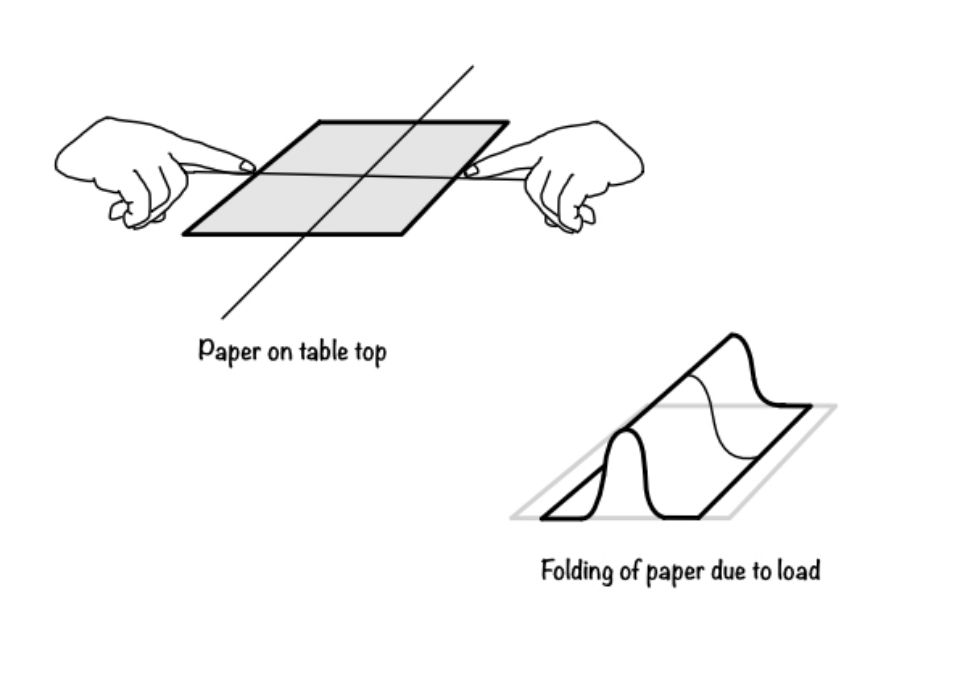
Now think about the paper. It has less lateral dimension than that length and width. Which leads to the buckling of paper. The same thing happens with structure. Hence, we first categorize them based on weakness in the lateral dimension. The term which does this is slenderness ratio.
What is the slenderness ratio?
The slenderness ratio is the ratio of effective length to the least gyration radius.
$$ S= \frac{L_{eff}}{r_{min}} $$
We generally divide the columns into long and short columns based on this ratio.
$$ S\le 12 \longrightarrow \text{Short Column}\\S> 12 \longrightarrow \text{Long Column} $$
You can refer to the article on the slenderness of columns to know more about how the effective length is calculated.
What is a long and short column?
You must be thinking about dividing the columns into long and short columns. This we do for the failure mode identification.
That means the short columns fail in the crushing failure, whereas the later dimensions are small in the long column. Hence long columns fail in buckling failure, as shown in the figure.
How buckling affects the column strength?
The strength of the column severely reduces due to the buckling effect. The buckling effect leads to catastrophic failure. Hence in the slender compression members, it is very important to know the load after which the buckling may occur.
How to calculate the critical load?
As we have discussed, that long column fails in buckling. To protect the column from buckling, we must know the load at which buckling failure may occur. We call this load a critical load. Determination of critical load for the column is very important for the long column. To help us in this matter, Euler gave the formula to calculate the critical load.
How to derive the Euler’s critical load?
In 1757 Swiss mathematician Leonhard Euler gave the theoretical analysis for the critical load formula. His analysis was based on the differential equation for the elastic curve:
$$ EI\frac{d^2y}{dx^2}=M $$
What are the limitations of Euler’s formula?
He made the following assumptions while deriving the theory for the critical load:
- This analysis is valid only up to the proportional limit.
- The deflection is so small that there is no difference between the deflected length and the column’s original length.
Application of elastic theory
From the free-body diagram of the column, as shown in the figure, we can calculate the moment in the column:
$$ M=Py $$
Substituting this value in the above equation:
$$ \frac{d^2y}{dx^2}+Py=0 $$
This is second-order homogenous differential equation. The general solution for this type of differential equation is as follows:
$$ y=C_1 \sin{\sqrt{\frac{P}{EI}}} x+C_2 \cos{\sqrt{\frac{P}{EI}}} x $$
The values of the constant can be determined from the boundary conditions:
In this case the value at $x=0$ ; $y=0$ and at $x=L$; $y=0$
When we put $x=0$ in the general solution:
$$ y=C_1 \sin{\sqrt{\frac{P}{EI}}} (0)+C_2 \cos{\sqrt{\frac{P}{EI}}} (0)\\y=C_2 $$
To make $y=0$ at $x=0$, the value of $C_2$ must be equal to zero. Similarly, for another boundary condition $x=L$,
$$ y=C_1 \sin{\sqrt{\frac{P}{EI}}}L \\ C_1 \sin{\sqrt{\frac{P}{EI}}}L=0 $$
This equation has two solutions. One $C_1=0$, which means for any value of $x$ the value of $y$ will be zero. This means the column is straight and does not have any sense. Hence this is the trivial solution.
Another solution will be:
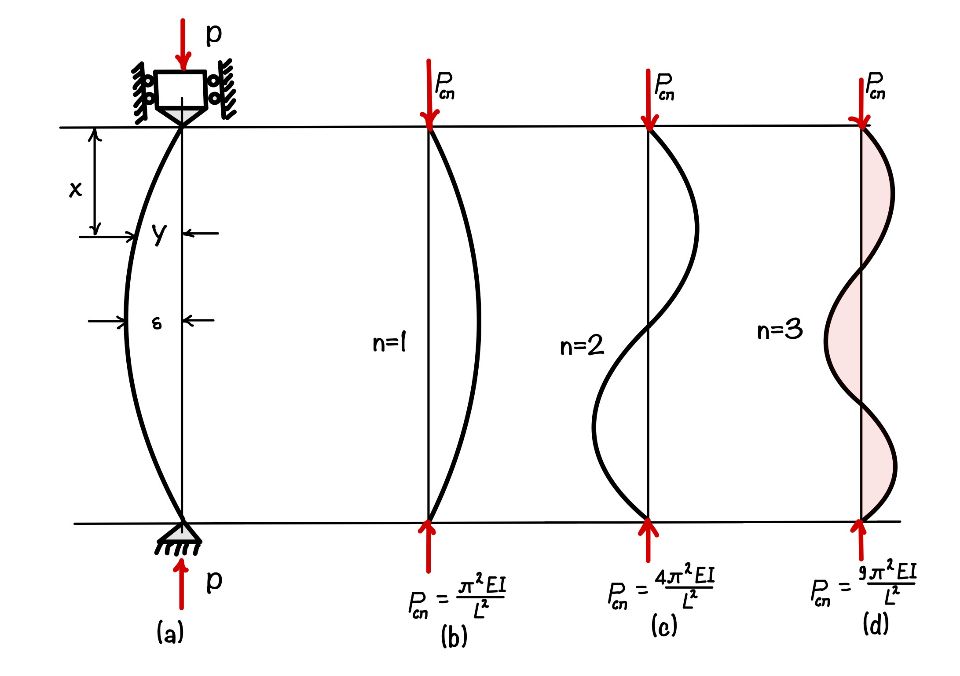
$$ \sin{\sqrt{\frac{P}{EI}}}L=0\\\sqrt{\frac{P}{EI}}L=n\pi \text{ for } n=1,2,3…n $$
Now rearranging this solution, we get the equation in the following form:
$$ P_{cr}=\frac{n^2\pi^2EI}{L^2} $$
This load is a critical load, and the equation is called Euler’s equation. This load is derived for the column with both ends pinned. We need to modify the formula for the columns with another type of support.
$$ P_{cr}=\frac{\pi^2EI}{\frac{L^2}{n^2}} = \frac{\pi^2EI}{L_{eff}} $$
Effective length in different cases
Now we can use this formula to calculate the critical load for any column. We need to put the effective length value for the respective end condition of the column.
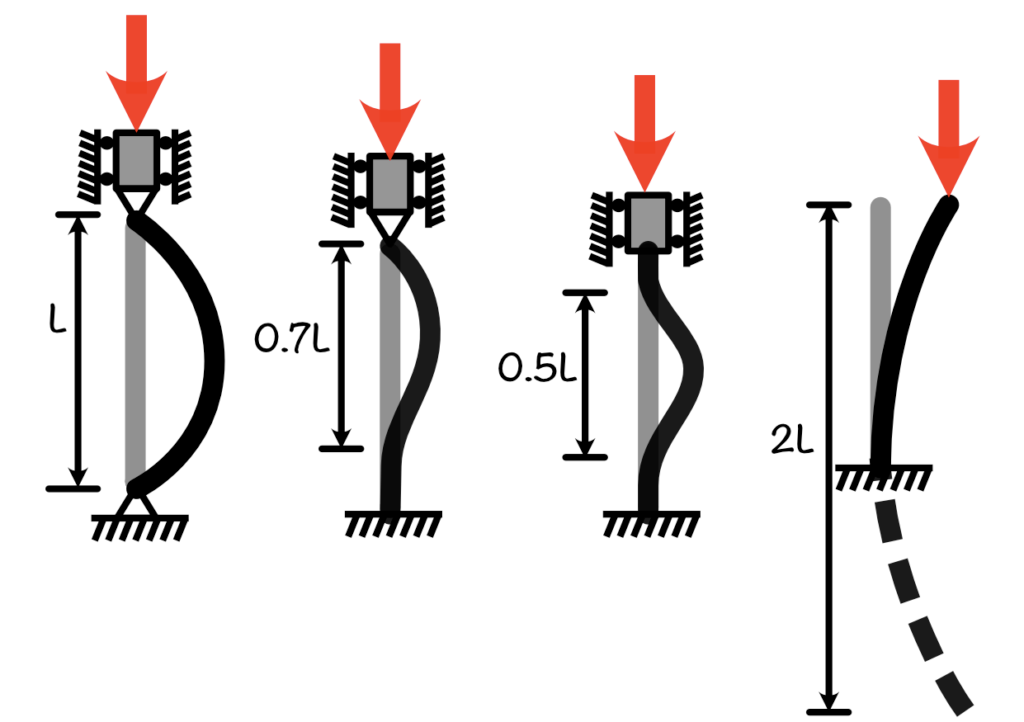
Here are a few values of the effective length of the column:
- Pin Pin: For pin-pin support, the effective length will be the length of the column only. (refer to figure)
- Fixed-Free: For the fixed-free end condition, the effective length of the column will be twice the length of the column. (see the fourth column in the figure)
- Fixed-Pin: The point of inflection for this column condition is $0.7L$ away from each other.
- Fixed-Fixed: For the fixed end conditions, the distance between the point of inflection is $0.5L$.
The equivalent length is the method to modify Euler’s formula for different end conditions of the column. We have to look for the point of inflection in the columns.
Conclusions
You know from the above discussion that the columns carry axial compressive loads. Based on the slenderness ratio, we divide the column into a long and short ones. Long columns fail in buckling. To evaluate the critical load for the pin-pin end condition column, Euler gives the critical load formula. Can you apply the Euler critical load formula in every situation?
In this post, you have learned the following key points:
- Slenderness ratio: It is defined as the ratio of effective length to the radius of gyration.
- Long Column: Based on the slenderness ratio, columns are divided into long and short columns. The column is categorized as a long column with a slenderness ratio of more than 12.
- Buckling: It is the out-of-plane bending in the structure.
- Euler Critical Load: Any column can sustain the critical load without buckling.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


