The stability of slender columns refers to their ability to resist buckling, which is a type of lateral instability that occurs when the compressive force exceeds the column’s capacity to resist it.
To give you an idea about the stability of the column, we will do a simple demonstration. First of all, make two paper tubes of different dia and keep them on the table. Place a weight on top of the tubes, making sure that the weight is centered over the tubes.
Then observe what happens, The smaller dia tube is likely to buckle under the weight, while the larger dia tube will remain stable. This simple demonstration illustrates the importance of the cross – sectional area in the stability of slender columns. A larger cross – sectional area means a larger moment of inertia, making the column stiffer and less likely to buckle under compression.
What is buckling of columns ?
It is the the critical load for a column, in pure buckling . By assuming that the beam acts as an ideal column, the critical load for the column is :
$$
P_{c r}=\frac{\pi^{2} E l}{\left(\beta L^{2}\right)}
$$
We can reduce buckling by reducing the length of the column. Bracing in columns can reduce the column length. The brace can be of two types: elastic or ideal. An elastic brace can take the load and deflect along with the bracing. The displacement is dependent on the stiffness of the brace, when it becomes stiff enough it will remain in place and be considered ideal.
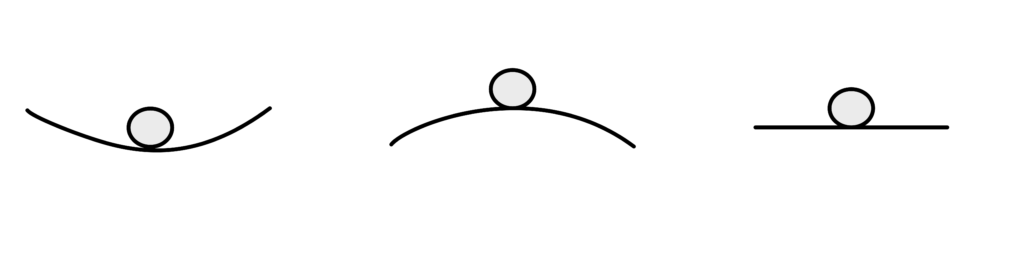
In the practical case, there are three main category of stability,
- Stable: When the value of load applied is less than the critical load (P < Pcr), the object will return to its original position, with no change in the column.
- Unstable: When the value of load applied is more than the critical load (P > Pcr), the object will move and will not return to its original position, Geometry changes.
- Neutral: When the value of load applied is equal to the critical load (P = Pcr), the object will move and stop at equil. position, i.e, the shape changes.
Failure of structures may be also because of geometric instability. In the case of a slender column, the slenderness or the stiffness of the column becomes more important. The capacity of material in the case of slender column is not fully utilized. The column fails due to buckling even before the column reaches the stress limit of the material.
How to improve stability of columns ?
We can improve the stability of slender columns in several ways:
- Increasing the c/s area of the column: A larger c/s area means a larger moment of inertia, which in turn makes the column stiffer and less likely to buckle.
- Strengthening the column material: Using high strength materials can improve the stability of slender columns.
- Reinforcing the column: The addition of bars or fibers can increase the capacity of the column to resist buckling.
- Using composite columns: Composite columns, made by combining two or more materials, can provide increased stability to slender columns.
- Reducing the axial load on the column: By reducing the load on the column, it becomes less likely to buckle under compression.
- Properly bracing the column: Bracing the column can provide lateral stability and reduce the risk of buckling.
- Increasing the length to dia. ratio: A larger length-to-diameter ratio makes the column more slender, which in turn increases the risk of buckling. To mitigate this, it is important to properly design the column and ensure that the length-to-diameter ratio is within the limits.
Conclusions:
In conclusion, the stability of slender columns is an important aspect of construction design and engineering. Additionally, it is important to consider the external loads and environmental conditions that the column may encounter.
Some of the take away of this post are as follows:
- Stability of column: The use of cross-bracing, large c/s dimensions, and the addition of reinforcement can effect the stability of columns.
- Factors to improve stability: Some of the ways by which we can improve the stability of column are increasing the c/s area of the column, proper bracing, inc. the length to dia. ratio, use of high strength concrete, etc.
Column design
- RCC Column Design is a free app for designing reinforced concrete columns as per Indian Standards.
- RCC Design and detailing could be performed for uniaxial and biaxial bending conditions specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


