To understand the concept of slenderness ratio, let’s consider a simple demonstration. Imagine two thin rods made of the same material, one that is very tall and one that is very short. When you apply a load to the top of the rods, you will notice that the taller rod is more likely to bend or buckle, while the shorter rod remains more stable (see the figure below).
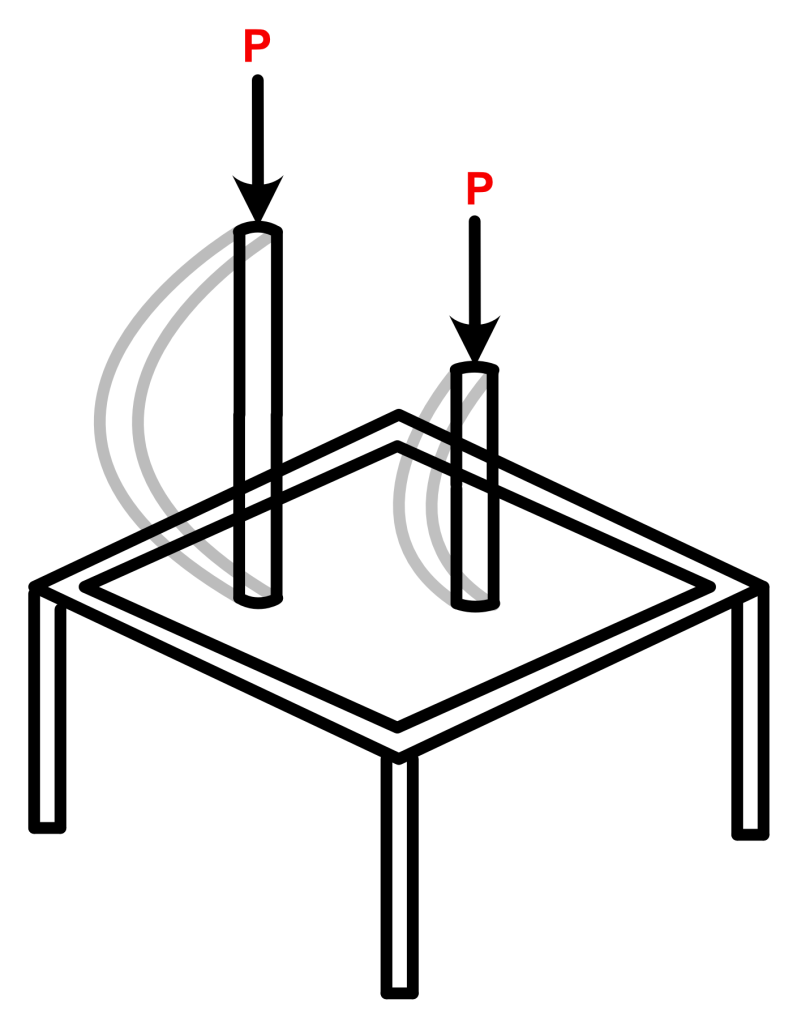
This difference in behavior can be explained by the concept of slenderness ratio – the taller rod has a higher slenderness ratio, making it more prone to bending, while the shorter rod has a lower slenderness ratio, making it more resistant to bending.
What is slenderness ratio ?
Slenderness ratio is a geometrical parameter, defined for a compression member (column). It is the ratio of effective length and lateral dimension of the compression member. It is also a measure of the structural vulnerability to the failure of the structure.
Slenderness ratio can also be defined as the ratio of effective length of the column to the minimum radius of gyration. Generally we design the columns to resist the axial compression load. Sometimes a combination of bi-axial/ uni-axial moment acting on it.
What is the basis of slenderness ratio formula ?
Columns are made to support compressive loads, this compressive load may cause buckling in the column which may lead to failure well before the compressive strength of the column. These compressive loads are connected with buckling phenomenon by Euler’s define the critical load formula.
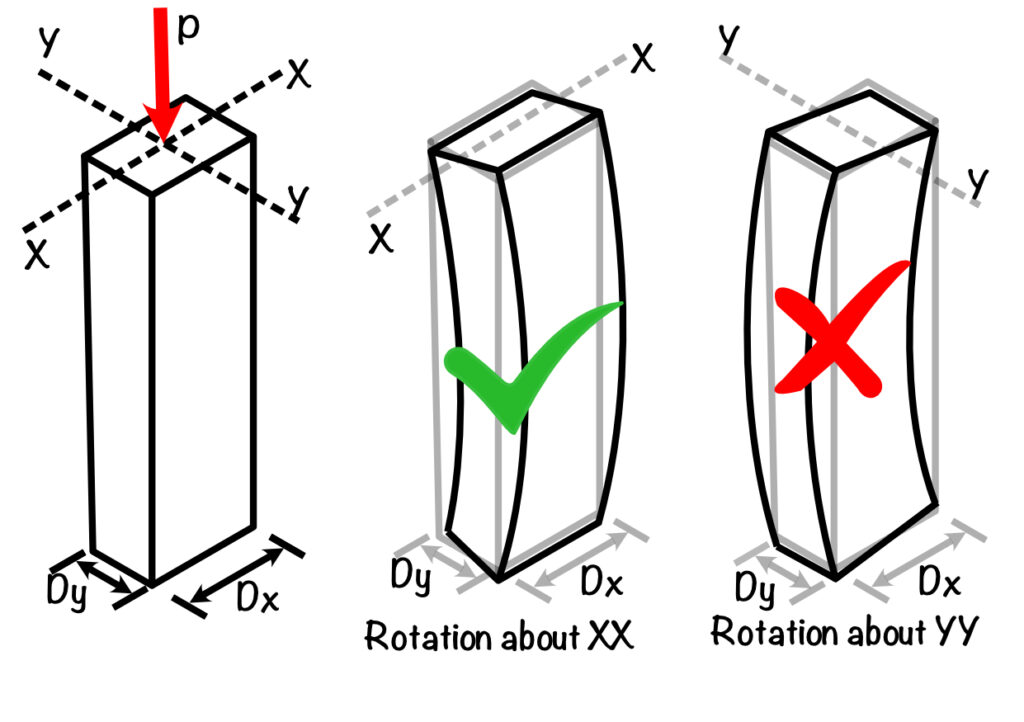
From the Euler formula, the slenderness ratio is inversely proportional to the radius of gyration. This means the tendency of buckling failure is maximum when r is minimum.
$$S \propto \frac{1}{r}$$
Slenderness ratio is also proportional to K lu, where K is the effective length factor and lu is the unsupported length of the column.
$$S \propto K \times l_u $$
$$ S \propto l_{eff} $$
Combining this both, we get :
$$\text{Slenderness ratio} = \frac{l_{eff}}{r_{min}}$$
Where: $l_{eff}$ is the effective length, and $r_{min}$ is the minimum radius of gyration.
Bending of column will depends on the radius of gyration. Column will bend in the direction where radius of gyration is minimum.
$$
r_{\min }=\sqrt{\frac{I_{\min }}{A}}
$$
On the basis of slenderness ratio, we classify the columns as :
- Short columns: The value of slenderness ratio is less than or equal to 12.
- Long or slender columns: The value of slenderness ratio is greater than 12.
What is Effective length ($l_{eff}$) ?
The effective length of a column is a measure of the length of the column that is involved in the buckling process. It is used to calculate the critical buckling load of a column, which is the load at which the column becomes unstable and buckles.
The effective length of a column can be different from its actual length, on the basis of the type of support and the loading conditions. Euler’s column formula is for pin end column hence load carrying capacity changes with change in support condition. Incorporate this change in support condition by the effective length as shown in below figure.
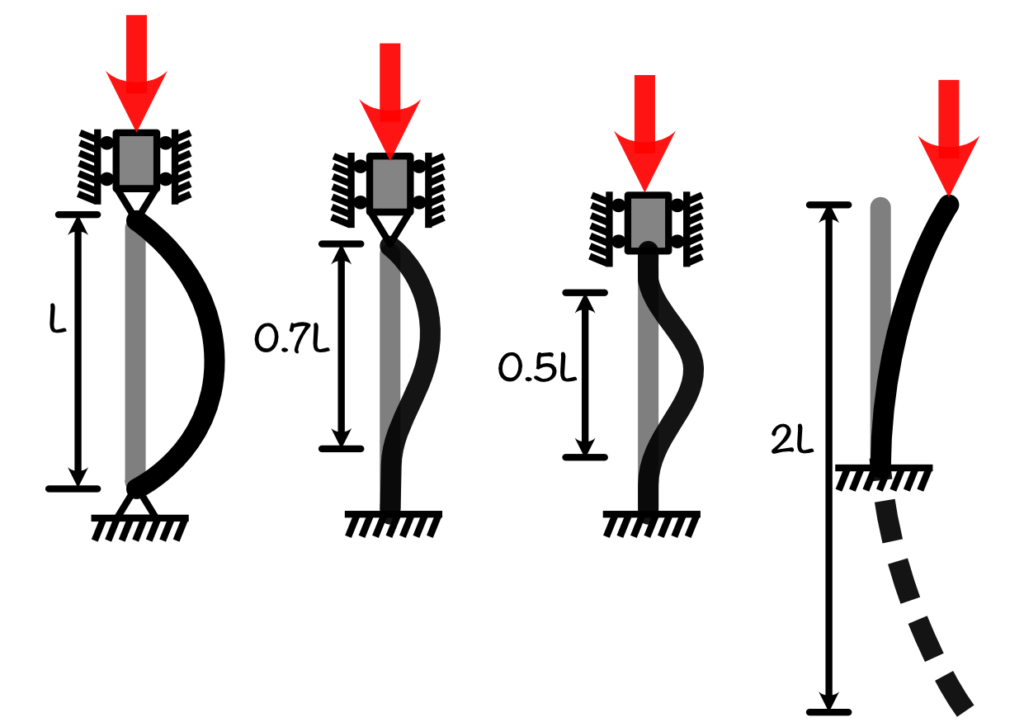
As you can see in the figure that we are choosing the length of the column which will behave like pinned end condition column.
What is the effective length of column according to IS:456 ?
In practical situation some more complexities comes in picture. There we can not defined ideal support condition as we have defined in the fig above. Hence code defined some rational number based on the experiments and concrete theories, which we need to follow.
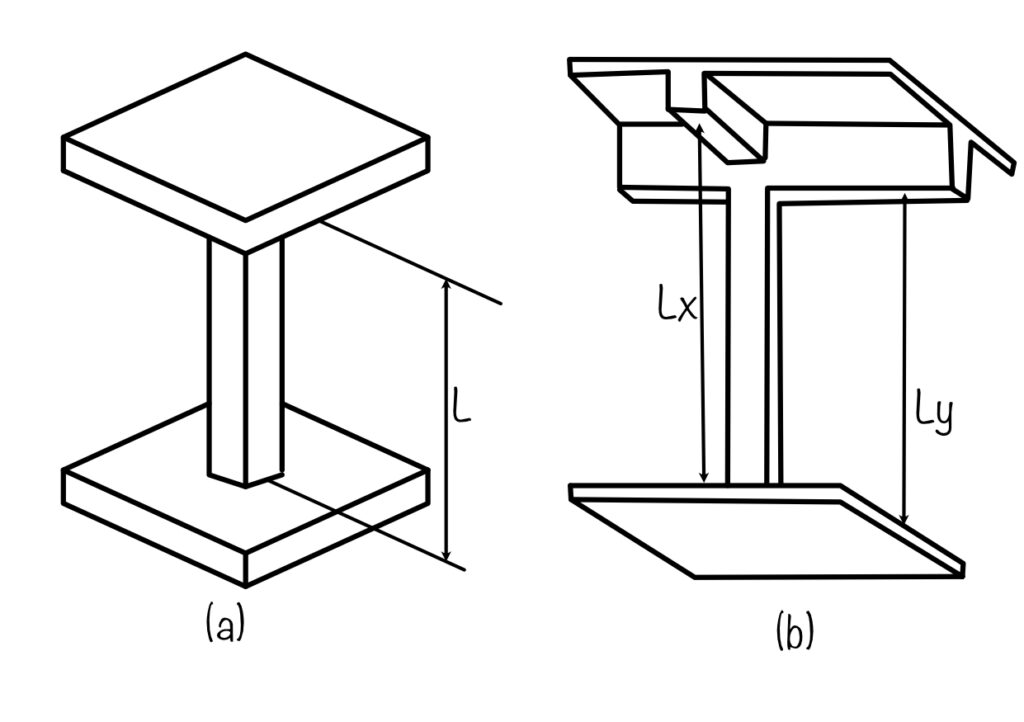
Code uses a term Unsupported length. According to Clause 25.1.3 of IS 456:2000 it is the clear height of the column. Figure below shows the unsupported length of column in different cases.
Where do civil engineers use slenderness ratio in actual design?
As a civil engineer, our main aim is to find the load which column can take before buckling failure, and this load depends on the slenderness ratio. The slenderness ratio also defines the failure mode of the column based on the effective length and the radius of gyration.
The design of RC columns section is done according to the codal provisions given in IS: 456-2000. By directly using the charts available in SP 16, one can design the columns section efficiently.
Check this post to read a brief about what is a column and what are the different types of column
Conclusions :
In conclusion, the slenderness ratio is an important factor to consider in the design of structures, particularly columns. When designing a structure, engineers must take into account the slenderness ratio to ensure that the structure will be able to withstand the loads it will be subjected to.
In this post, you have learned the following key points:
- Effective length: It is used to calculate the critical buckling load of a column.
- Failure mechanism: Slenderness ratio decide the failure mechanism of column weather column will fail in crushing failure or in buckling failure.
- Minimum radius of gyration: Column will buckle in the weak side first if we use minimum radius of gyration.
- Failure of materials: Columns with low slenderness ratio, fails as a result of failure of materials. i.e., this structure fails when concrete or steel reaches its ultimate strength and not due to buckling. On the other hand columns with high slenderness ration, the structure fails mainly due to buckling along with large lateral deflection.
Column design
- RCC Column Design is a free app for designing reinforced concrete columns as per Indian Standards.
- RCC Design and detailing could be performed for uniaxial and biaxial bending conditions specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author



Great
Thank you for your appreciation. Please say Hi to us in Linkedin, and give some suggestions on the topic you would like to see on our website.
helpful