The volume of the system remains unchanged throughout an isochoric process, which is a thermodynamic process. The pressure cooker in which you cook your food or the engine of your bike that you use to commute around, are the common example that works in an isochoric process where the volume is constant.
For instance, an isochoric combustion process can lead to a more thorough burning of the fuel in an internal combustion engine, increasing power output and fuel efficiency. The isochoric process is a fascinating topic in thermodynamics and a crucial idea for comprehending how systems behave in the actual world. It is amazing to discover the many real-world uses and consequences of this method, which have a significant influence on the development and performance of many engineering systems.
Definition of the Isochoric process
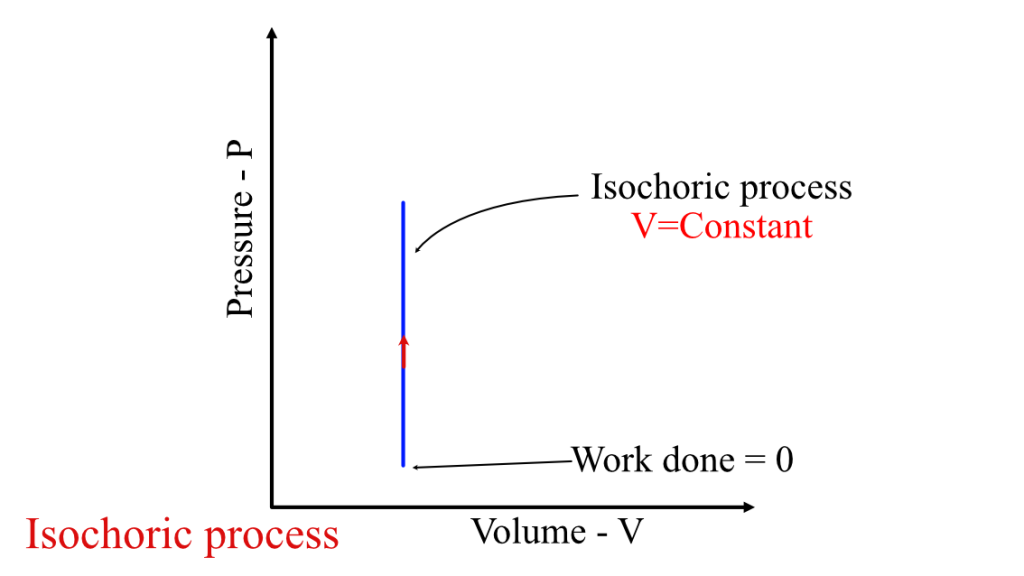
An isochoric process is a thermodynamic process in which the volume of the system remains constant. Mathematically, this can be represented as:
$$ V = \text{Constant}$$
During an isochoric process, no work is done by the system as there is no change in volume. Therefore, the first law of thermodynamics for an isochoric process can be represented as
$$Q = \Delta U$$
where $ \Delta U$ is the change in internal energy of the system, and Q is the heat added to or removed from the system.
In an isochoric process involving an ideal gas, the ideal gas law $PV = nRT$ still holds. The change in internal energy of an ideal gas can be computed using the following equation $ΔU = nCvΔT$ where $C_v$ is the heat capacity at constant volume and n is the number of moles of gas.
Work done in the Isochoric process
In a closed system, the work done by the system is given by the equation:
$$W = -P \Delta V$$
However, in this process, the volume of the system is constant, so $ΔV = 0$. Therefore, the work done by the system in an isochoric process in a closed system is:
$$W = -P(0) = 0$$
In other words, no work is done by the system during an such process in a closed system, as the volume of the system does not change and therefore there is no movement of the piston in the cylinder.
Practical examples
The engineering applications of these processes are everywhere, from the engine of your scooter or bike to the refrigerators that you use to store ice creams or cold drinks.
Here are a few practical engineering examples of isochoric processes:
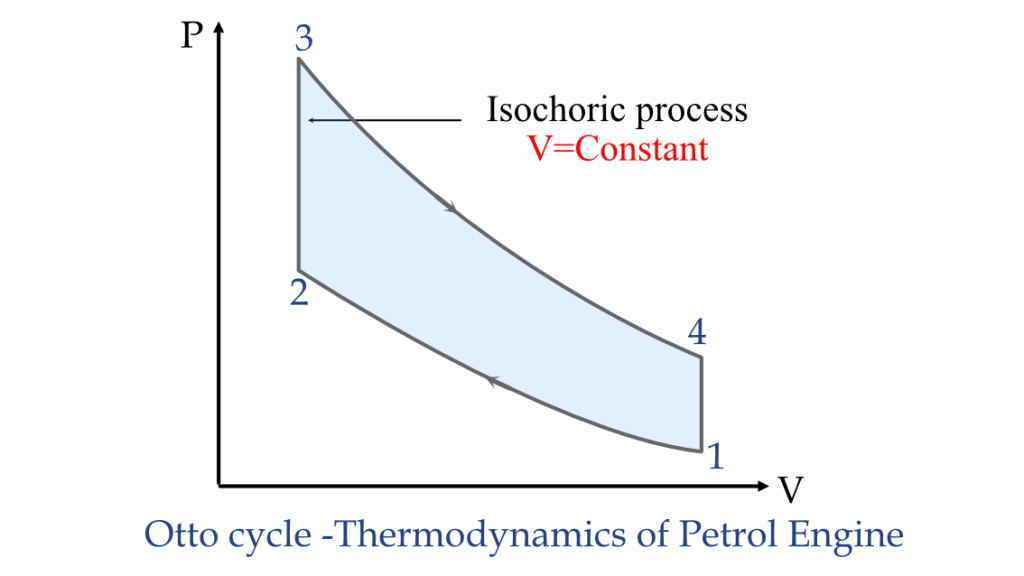
- Internal combustion engines: During the compression stroke in an internal combustion engine, the volume of the cylinder is kept constant by the piston. Thus, the combustion process that occurs is an isochoric process.
- Gas storage tanks: Storing gas in a tank at high pressure is an isochoric process, as the volume of the gas does not change, only the pressure.
- Fuel cells: The reactions that occur in a fuel cell can be thought of as an isochoric process, as the reaction occurs at constant volume and pressure inside the cell.
- Refrigeration systems: During the evaporative stage of refrigeration systems, when the refrigerant evaporates and absorbs heat, it occurs at constant volume.
- Constant-volume calorimeters: These devices are used to measure the heat of chemical reactions, and they work by maintaining a constant volume so that any energy added or removed from the system can be attributed to a change in internal energy.
Isochoric process and ideal gas
it’s important to note that the relation between P, V, n, T, and R may be different depending on the specific process that is taking place.
In addition to that, The internal energy of an ideal gas is related to its temperature, and for an ideal gas in an isochoric process, the change in internal energy is given by:
$$ \Delta U = nC_v \Delta T$$
Where $C_v$ is the heat capacity at constant volume and $\Delta T$ is the change in temperature, and n is the number of moles of gas. This relation is consistent for such a process for ideal gas only.
It’s important to keep in mind that these formulas only hold for an ideal gas, which is a theoretical concept and does not exist in reality. Real gases deviate from the ideal gas law under certain conditions.
Conclusions
An isochoric process is a thermodynamic process where the volume of the system is constant, this implies that the work done by the system is zero, whether the system is open or closed. The ideal gas law $PV = nRT$ is valid in this case, and the change in internal energy of an ideal gas can be computed using the equation $ΔU = nC_v \Delta T$, where $C_v$ is the heat capacity at constant volume and ΔT is the change in temperature.
Some key learnings from the post are:
- Definition: Isochoric process is a thermodynamic process where the volume of the system is constant.
- Work done: Work done by the system is zero, whether the system is open or closed.
- Isochoric process and Ideal gas: Change in the internal energy of an ideal gas can be computed using the equation $ΔU = nC_vΔT$.
- Applications: Many real-world engineering systems can be modeled as an isochoric process such as internal combustion engines, gas storage tanks, fuel cells, refrigeration systems, and calorimeters.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


