If you want to know what is column or compression member, pick up the pencil in the table in front of you, now try to compress it as shown in the figure. See, you have one compression member in your hand. This pencil is now behaving as a compression member.

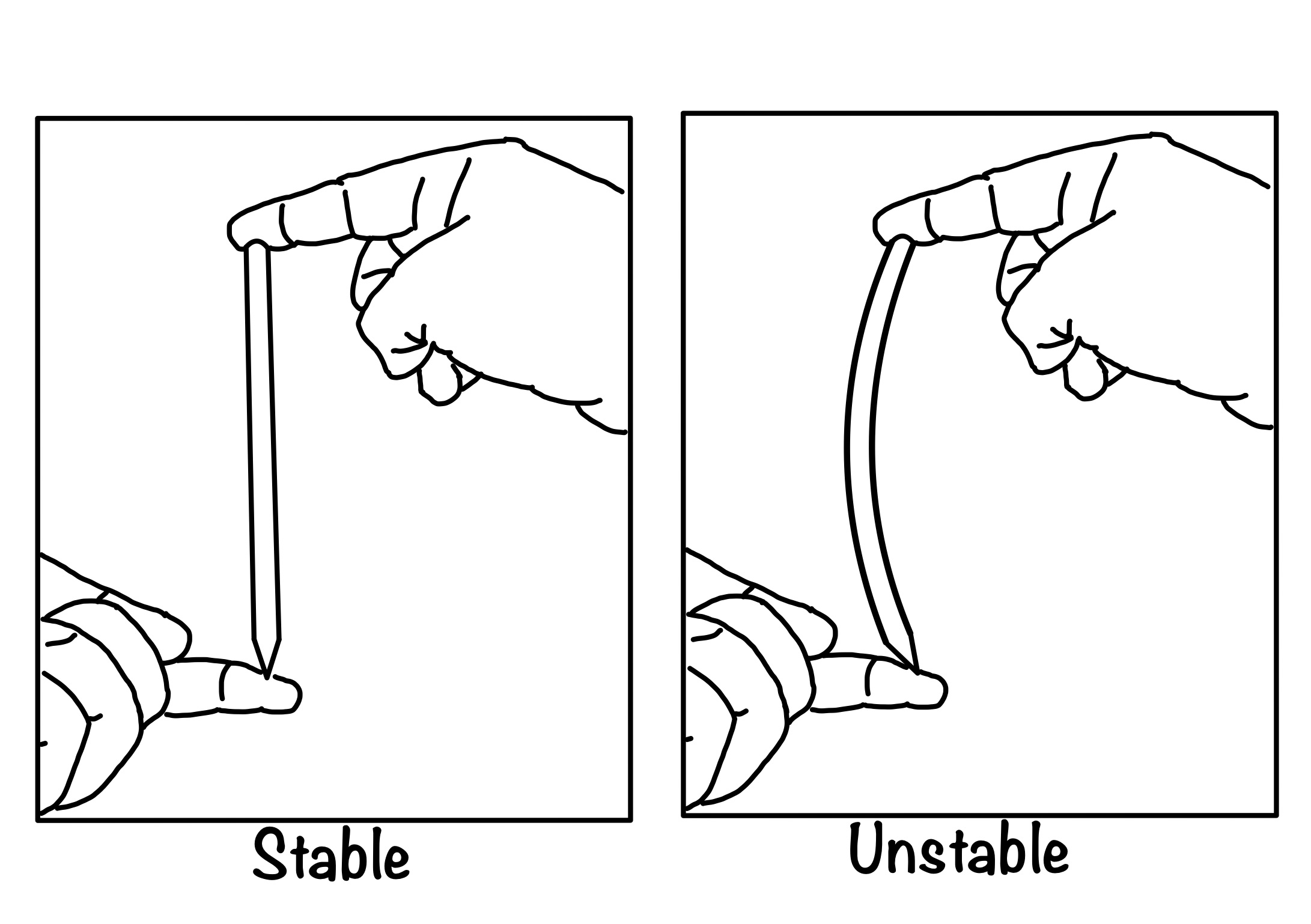
Then you must think about why we are so bothered about the load-carrying capacity of the compression members. Simply, multiply the cross-section area by the strength of the column and you will get the force that this column or compression member can take.

Here comes stability, which plays an important role in the case of compression members. It reduces the strength of the compression member. Hence we need to check the strength of the compression members.

In this article we will learn about the different types of compression members, what are the important factor in the design of compression members. We will also learn the important steps in the designing of the compression members.

Classification of the compression members

Compression members are those who takes compression. We classify them for our convenience so that we can understand the different types of members.

Compression members can be classified as follows:

Columns: These are straight members subjected to heavy compressive loads. Columns always remains vertical.
Strut: It is the compression members which can be tilted or horizontal. This type of compression members are subjected to light vertical loads.
Boom: These are the main members of the crane as you can see in the figure.

Importance of stability in the column design

The main issue in the design of column is the stability. Generally when you will apply the load in the column it resist the load till the stress generated by the column is less than the strength of the column. But the instability in column reduces the strength of the column.

Hence, our main aim in the column design is to calculate the strength of the column. This strength depends on the degree of stability of the column. Now question arises how to decide the degree of stability of the column?

Don’t worry the different specific provision defined by different codes of the different countries takes care of it.

If we want to calculate the strength of the column according to IS:800-2007 steps are as follows:

Classification : Based on the section of the column we will decide the buckling class of the section from Table – 10 of IS 800:2007.
Material: Based upon the material used to build the column we will fix the strength of the column.
Stability: Now we will modify the strength of the column based on stability.

To check detailed procedure of how to do this please read the complete article.

Slenderness ratio: Only ingredient to compute design stress $f_{cd}$

In order to design a compression members, you need essentially one thing: Slenderness ratio of the member ($\lambda$). The tendency of a member to buckle (sudden change in geometry due to small change in load) is usually measured by slenderness ratio ($\lambda$) where,

$$ \lambda = \frac{KL}{r} $$

where, $K$= Effective length factor; $L$= Length of the member; $r$=radius of gyration= $\frac{I}{A}$ where $I$=Moment of Inertia about axes of the cross-section; $A$= Area of cross-section

As per IS 800:2007, the design compressive stress $f_{cd}$ is given as:

$$ f_{cd}=\frac{f_y/\gamma_{m0}}{\phi+[\phi^2-\lambda_e^2]^{0.5}}=\chi f_y/\gamma_{m0}\leq f_y/\gamma_{m0} $$

where,

$\phi=0.5[1+\alpha(\lambda-0.2)+\lambda^2]$

$\alpha=$ Imperfection factor given in Table 7, IS 800:2007

$\lambda_e=$ non-dimensional effective slenderness ratio $=\sqrt{f_y/f_{cc}}$

$f_{cc}=$ Euler buckling stress $=\frac{\pi^2E}{(KL/r)^2}$

$\chi=$ Stress reduction factor given in Table 8 IS 800:2007

$\gamma_{m0}=$ Partial safety factor for material strength $=1.1$ (from Table 5, IS 800:2007)

The calculated value for different buckling class is given in Table 9, IS 800:2007.

 Note: The compressive design stress $f_{cd}$ can be calculated directly from Table 9 for all cross-sections except for single-angle sections.

Note: The above equation formulation is valid for all sections (I-section, Channels, etc.) but not for single-angle sections.

$$ \lambda_e=\sqrt{k_1+k_2\lambda_{vv}^2+k_3\lambda_{\psi}^2} $$

The definitions of $k_1, k_2, k_3, \lambda_{vv}, \lambda_\psi$ are given in Clause No. 7.5.1.2, IS 800:2007.

Remember: Higher the slenderness ratio, $\lambda$; Lesser the design compressive strength, $P_d$.

Design Example: Calculating the compressive strength

Determine the compressive strength for the member shown below. Assume steel of grade Fe 410 $(f_y=250\; MPa)$.

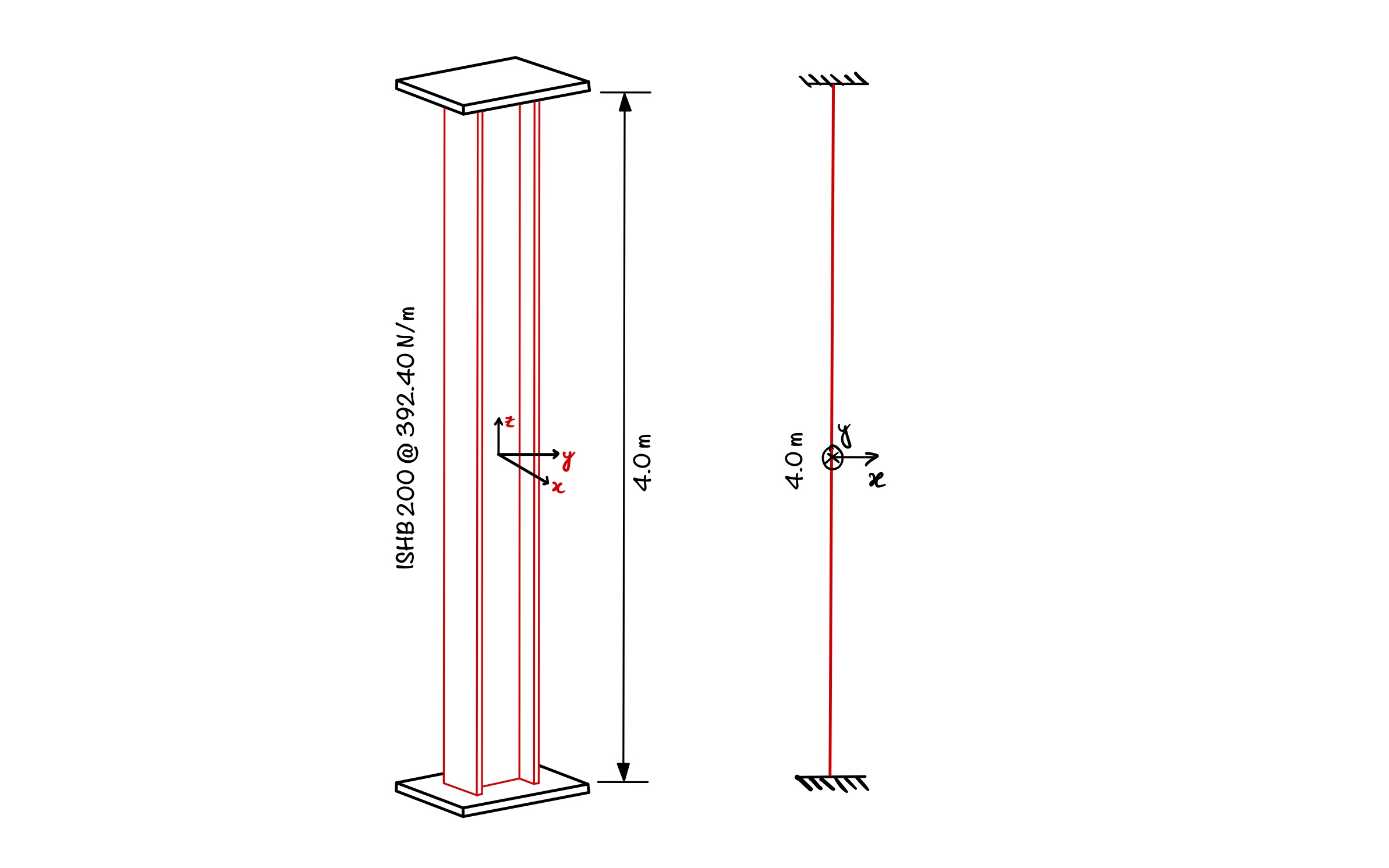
Let us solve the problem step-by-step.

Step-by-step procedure

Step 1: For any given problem, search for the section in SP: 6(1) and note down the cross-sectional properties such as Area of cross-section $(A)$, Moment of inertia about both axes $(I_{xx}, I_{yy})$, radius of gyration about both the axes $(r_{x}, r_{y})$.

For the given section, ISHB 200 @392.40 N/m:

$$ A=5094 mm^2 \\ I_{xx}=3721.8\times 10^{4}mm^4 \quad I_{yy}=994.6\times 10^4 mm^4$$

$$ r_{x}=85.5mm$$ $$r_{y}=44.2mm $$

Step 2: Check for the boundary condition of the given problem to determine effective length, $KL$. Refer to Table 11, IS 800:2007 for value of $K$ for various boundary conditions.

We can see the boundary condition of the problem is fix-fix. Thus, referring to Table 11, IS 800:2007 for restrained – restrained conditions, $KL=0.65L=0.65\times 4000=2600\;mm$.

Reduction in strength

Step 3: Calculate slenderness ratio $\lambda_x; \; \lambda_y$

Now,

$$ \lambda_x=\frac{2600}{85.5}=30.41;\quad \quad \lambda_y=\frac{2600}{44.2}=58.82 $$

Taking maximum value, $\lambda_y=58.82$. (Minor axis buckling)

 Note: A column can also undergo major axis buckling under different circumstances. Can you wonder how?

Step 4: Determine the buckling class for the compression member

Table 10, IS 800:2007 provides buckling classes of cross-sections based on:

Imperfection of the member (Residual stresses, initial bow, accidental eccentricity)
Type of buckling (Flexural buckling, Flexural-Torsional buckling)

For determining the buckling class, we need ratio of depth of the section and breadth of the flange i.e., $h/b_f$ and thickness of flange, $t_f$.

For the given section, ISHB 200 @392.40 N/m:

$$ h=200\; mm; b_f=200\; mm; \; t_f=9\; mm; \; t_w=7.8\; mm $$

Hence,

$$ \frac{h}{b_f}=\frac{200}{200}=1.0 $$

$$t_f=9\; mm \le 40\; mm $$

From Table 10, buckling class for minor axis buckling (y-y) is “buckling class b”.

Step 5: Select the suitable Table from IS 800:2007 to determine compressive stress $f_{cd}$ and hence design compressive strength $P_d$

The given problem is for “buckling class b” therefore select Table 9(b), IS 800:2007.

For the computed $\lambda=58.82$ and $f_y=250 \; MPa$, $f_{cd}=182.53\;MPa$

Design compressive strength,

$$ P_d=A\times f_{cd}=5094\times 182.53=930 \; kN \; < A\times f_y/\gamma_{m0} = 1158 \; kN $$

Conclusions

In this article, we discussed the easy steps for determining design compressive strength as per IS 800:2007. It is worthy to note that $P_d$ is less than yield strength of column, $A\times f_y/\gamma_{m0}$. This suggests that strength of the column is based on stability.

After reading this article you have learned the following key points:

Compression members: You have learned how many different types of compression members are there. You have also learned the difference in them.
Strength: The strength of compression members is governed by stability. Hence it is very important to consider the stability issues while calculating the strength of the compression members.
Slenderness ratio: You have learned how you can calculate it and how it affect the strength of the column.
Design strength: You have also learned the calculation of design strength of the column by an example.

Android Apps

⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)

At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.

Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.

KNOW MORE

This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are: