You must agree that bond stress is the main parameter on which development length depends. In this post, we will see the bond stress value for different grades of concrete. Apart from that, there are many other factors we need to cover as far as development length is concerned. Like development length for the bundled bars. Anchorage values for hooks and bends. We will also discuss the reduction in development length due to excess reinforcement.
What are the critical sections for development length?
You must know the general point, which is very critical for development lengths. These are the points where the flexural members are at the maximum stress or the point where the reinforcements are being terminated.
These are a few critical locations where you need to check the development length:
- Maximum moment: The point of maximum moment is the most common critical location where we need to perform the check.
- Cut-off: The point where your reinforcements are being terminated. Here you need to check.
- Lap Location: The point where you are providing the lap in the reinforcement. Here we need to ensure that proper stress transfer is happening.
- Support: At the simply supported beam, or cantilever beam, you need to check near the support and at the point of contra flexure. Contraflexure is the point where the bending moment changes the sign. Also at the
- Beam-Column: The beam-column junction is the most crucial location for the development length.
- Stirrups: Stirrups and transverse ties also need to check for development length.
Bond stress, according to IS456
IS456 in clause 26.2.1 gave the formula to calculate the development length.
$$ L_d=\frac{0.87f_y}{4\tau_{bd}}\times \phi $$
Where: $F_y$ is the yield stress in the bar, $\phi$ is the diameter of the bar, and $\tau_{bd}$ is the bond stress. The value of the bond stress is given in the IS456
| Grade of Concrete | M20 | M25 | M30 | M35 | M40 and Above |
|---|---|---|---|---|---|
| Design bond stress $\tau_{bd}$, MPa | 1.2 | 1.4 | 1.5 | 1.7 | 1.9 |
The above values may be increased by $60\%$ for the deformed bars. IS456 also suggests the increase in bond stress by $25\%$ for the bars in compression. For the nominal reinforcement, the bond stress is taken as $1.0$ $\text{N/mm}^2$.
Let’s discuss one more point in the calculation of development length and how this $0.875f_y$ comes in. If we understand the concept from physics, we need the actual stress in the bar. This stress in the bar multiplied by the area of the bar will give the force applied in the bar. This force in the bar needs to be balanced by the bond stress in the bar, as shown in the figure.
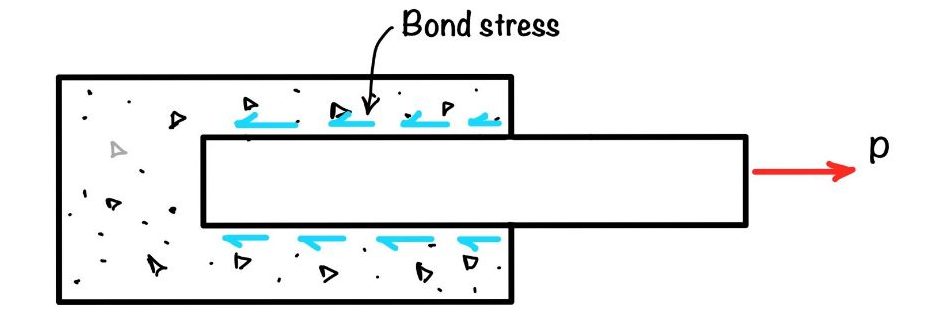
Now it’s very difficult to determine the actual stress in the bar, and the confidence is also low. So IS code suggests taking the full capacity of the bar so that you will get rid of stress calculation and the safety is also increased.
Development length for bundled bars
Multi-story buildings, skyscrapers, bridges, and heavy structures may need reinforcement. In the heavily reinforced section, there might be spacing problems. In those cases, we generally use bundled bars.
Bundled bars may have the following advantages:
- Space saving: Bundled bars help save space and reduce congestion for the placement and consolidation of concrete.
- Capacity enhancement: The bundling of bars provides better bending and orientation to bars which finally increases the capacity of the section.
- Tie bars: Bundling of bars requires less number of tie bars. Hence it helps in cost saving also.
While using the bundled bars, you should remember the following thing:
- Number of Bars: When you try to bundle the bar for any section, you should ensure they are in contact. And for the beam, you may limit the number of bars to $3$, and for the column, you may limit up to $4$.
- Size of bars: Using very large bars may lead to problems in crack control. Hence IS 456:2000 in clause 26.1.1 restricts the dia of the bar to $32$ mm. At the same time, the ACI restricts the bard diameter to $36$ mm.
- Positioning: Always keep the bundled bars within the ties.
- Monolithic: To ensure the monolithic action of the bundled bar, you should ensure they are tied together.
You can treat bundled bar as a single bar for development length calculations. Here we are giving you the equivalent diameter and perimeter of bundle bars. The formula used to calculate the development length is:
$$d_{eq}=d_b\sqrt{n_b}$$
| Bar Diameter $(d_b)$, mm | Equivalent Diameter, mm | ||
|---|---|---|---|
| Two-bar Bundle | Three-bar Bundle | Four-bar Bundle | |
| 12 | 16.97 | 20.78 | 24 |
| 16 | 22.63 | 27.71 | 32 |
| 20 | 28.28 | 34.64 | 40 |
| 22 | 31.11 | 38.11 | 44 |
| 25 | 35.36 | 43.30 | 50 |
| 28 | 39.60 | 48.50 | 56 |
| 32 | 45.25 | 55.43 | 64 |
Development length by providing anchorage
We have discussed how much development length is required for the safe design. Now let’s discuss how we generally provide the development length and what are the common practices.
Generally, we perform a few checks to provide development length in the beam. We provide bends or anchorage in the reinforcement if we do not have sufficient length available. But this remedy will not help in case of development length in compression.
For the different cases, we are providing the anchorage values in the table below.
| Bar Diameter, $d_b$,mm | 6 | 8 | 10 | 12 | 16 | 20 | 22 | 25 | 28 | 32 | 36 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anchorage value of hook, mm | 96 | 128 | 160 | 192 | 256 | 320 | 352 | 400 | 448 | 512 | 576 |
| Anchorage value of $90^\circ$ bend, mm | 48 | 62 | 80 | 96 | 128 | 160 | 176 | 200 | 224 | 256 | 288 |
Conclusions
In this post, we have discussed the bond stress and some critical parameter of the bond stress values. After that, apply the development length concept in more practical situations like bundled bars. We also learned ways to increase the development length by anchorage and bends. But this is not all. There might be a more difficult situation in the field. The most common problem is shortening og bar length. How to address this problem read in the Splicing article.
In this post, you learned the following key points:
- Bar strength: IS456 suggests that the full capacity of bars should be used to calculate the required development length.
- Bundled bars: To calculate the development length for bundled bars, we need to calculate the equivalent diameter.
- Bond stress: You must increase the bond stress by $60\%$ for deformed bars and $25\%$ for bars in compression.
Column design
- RCC Column Design is a free app for designing reinforced concrete columns as per Indian Standards.
- RCC Design and detailing could be performed for uniaxial and biaxial bending conditions specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


