When we pull on a reinforcement bar, it needs a certain amount of length in order to have a strong grip. This is known as the development length. It’s important to note that development length is also important when the bars are under compression. In this case, the length requirement is less compared to when the bars are in tension. You can think of it like it’s easier to remove a nail by pulling it out of the wall, rather than trying to push it in.
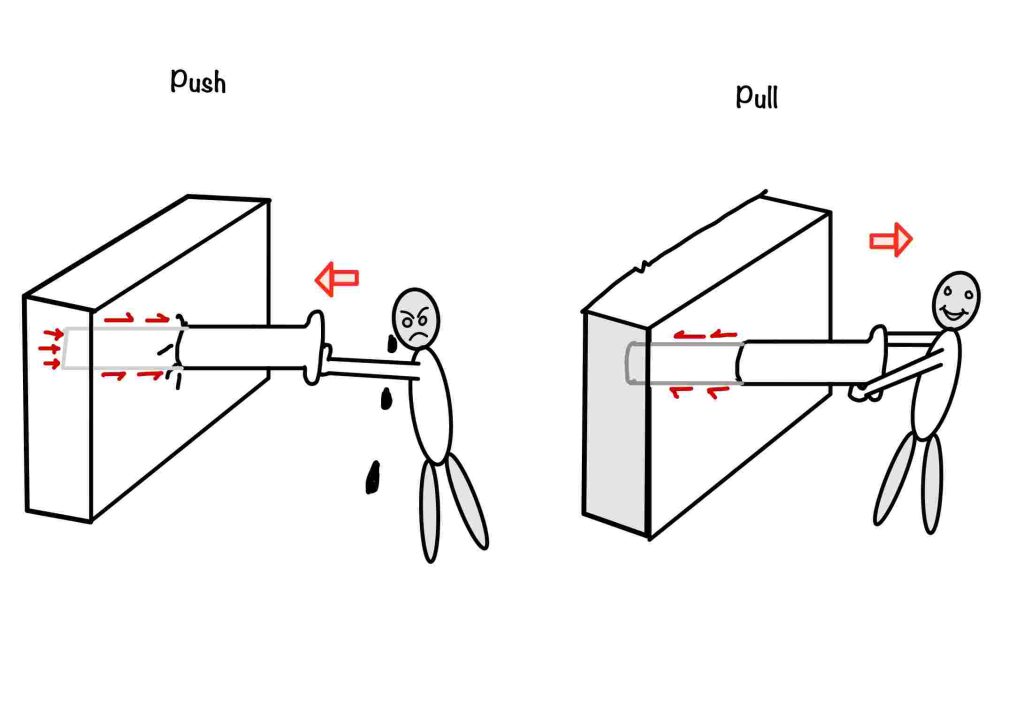
Hence from the above discussion, we can conclude that the length required to develop the grip in compression is lesser than tension. However, other factors are also responsible for the requirement of development length. In this post, you will learn the factors affecting the development length in compression, how much you have to reduce, and the IS code guidelines.
Factors affecting the development length in compression
When you design columns, the bars are in reduction. This is the most common situation where you can relate to the discussion. The actual behavior of the bar in compression is not known. Although few points are considered.
- End bearing: The bar in compression also benefits from the rod’s end bearing. However, the IS code has no formula to calculate the end bearing.
- Bond of concrete: The bond between the concrete and steel is also better in compression. This is because the tension crack in concrete is absent.
To address this effect IS-456:2000 increased the bond stress in compression by $25\%$.
Development length in compression by other codes
US, Canadian, and New Zealand codes specify the following formula to calculate the development length in tension.
$$ L_{dc}=\frac{0.286f_y\phi}{\lambda \sqrt{f_{ck}}}\ge0.043f_y\phi \text{ or 200 mm} $$
Where, $f_y$ is the yield stress, $\phi$ is the diameter of the bar, and $f_{ck}$ is the characteristic strength of the concrete. Where excess reinforcement is provided or confining reinforcements are there, the development length requirement reduces.
? When we compare the development length in compression required by Indian standard and other (US, New-Zealand, Canadian) codes. The Indian code provide $1.5-1.8$ times greater than others.
Development length in compression by anchor
Indian code suggests that you don’t have to consider the equivalent length due to the anchor. Instead, they mentioned that you have to ignore the length due to the anchor and only consider the projected length, as shown in the figure.
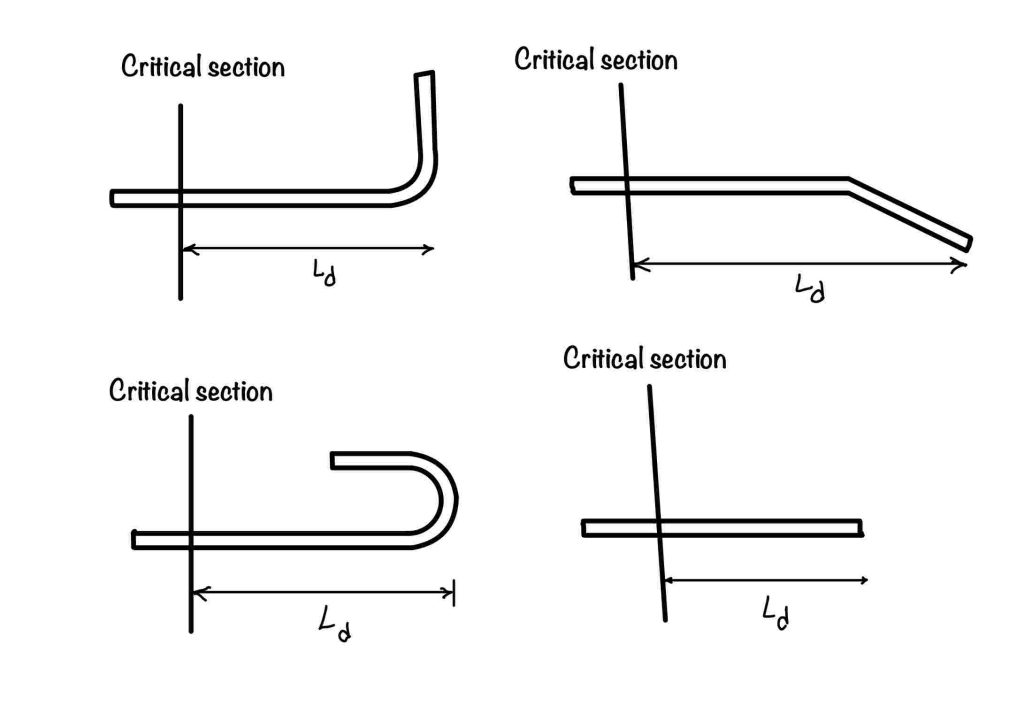
As you can see in the figure, we are considering only the projected length.
Conclusions
You have seen that the development length in compression is lesser than in tension. For example, the Indian standard code increases the bond stress by $25\%$. Other countries code suggested a formula to calculate the length.
In this post, you have learned the following key learning points:
- IS code: Bond stress in compression is increased by $25\%$ to calculate the development length.
- Other codes: Other codes give the formula to calculate the length required. They also gave the modification for the confining reinforcement.
- Anchorage: While considering the development length in compression, you have to consider only the projected length.
- Comparison: Indian standard provides $1.5-1.8$ more length when compared with the other countries’ code.
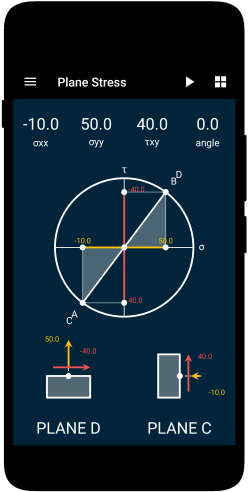
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.