When you load the column about its axis means the action line of load and the centroid of the column are coinciding then it is called the cocentrically loaded column. But when these axes are not in one line these type of loading is called eccentrically loaded column. In this post we will learn the stresses in the eccentrically loaded column and kern of the section.
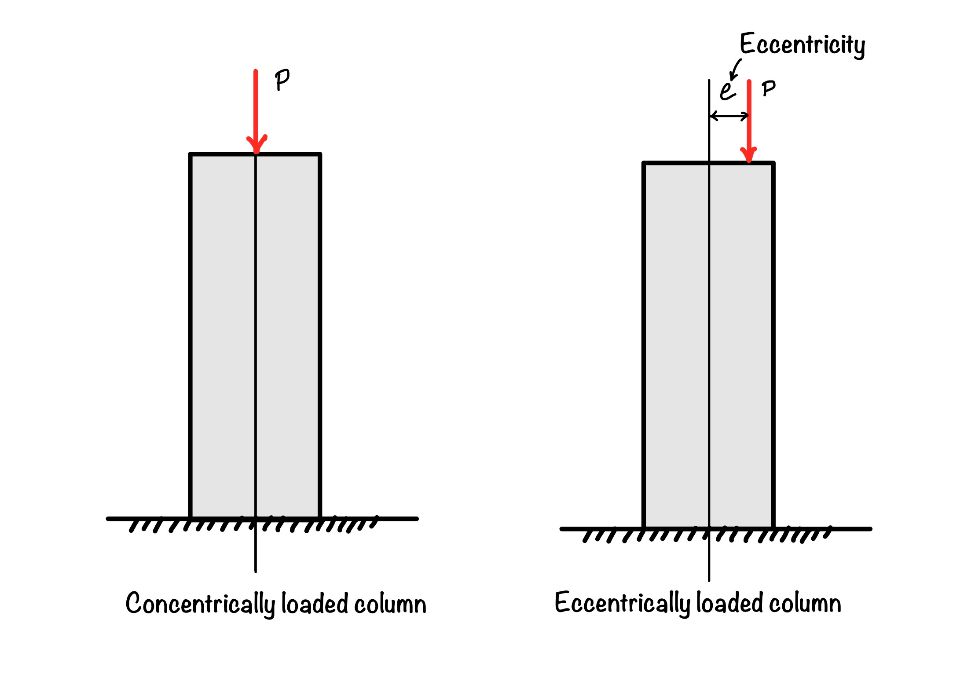
What are the stresses in eccentrically loaded column?
You now know the eccentrically loaded columns. If you see the figure below, you can conclude that the eccentric force creates moments and axial compression in the column. Stress generated in the compression is direct compression and the stress due to the moment is bending stress.
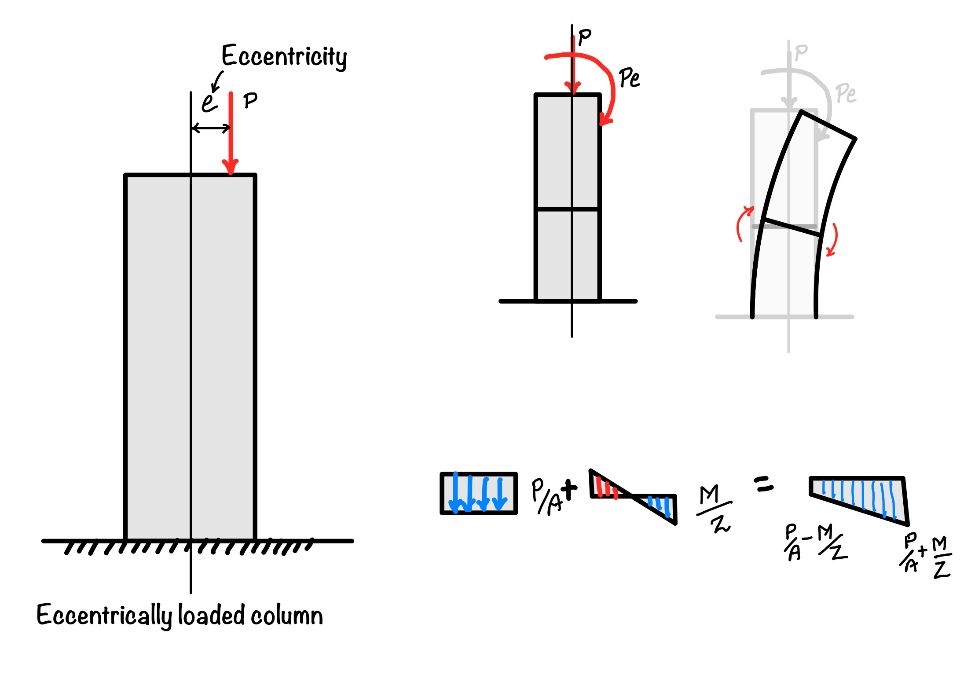
When column is eccentrically loaded following action will happen:
- Direct Compression: The effect of load in the axial direction will cause the compressive stress. The value of the stress will be $$P
- Bending stress: As we have already discussed in the bending stresses in beam the stress due to the bending varies linearly and you can find out it from $M/I =\sigma/y$ .
- Combined effect: In one end of the column they will be added and in other side of the column they will get deducted.
Please refer the figure for complete understanding of the expressions below:
$$ \sigma=\frac{P}{A} \pm \frac{M}{I}y $$
What do we mean by kern of a section?
Earlier the masonry structures were very popular. The property of the masonry structure is that they can not take tension. Hence the dams, chimney, retaining walls any many more structures. Hence we have to make sure that there is no tension stress in the column.
To assure this we have to make the minimum value of combined stress zero or more than that. This can be expresses as:
$$ \frac{P}{A} \pm \frac{M}{I}y \ge 0 $$
The region of load application which full fill the above condition is core or kern of the section.
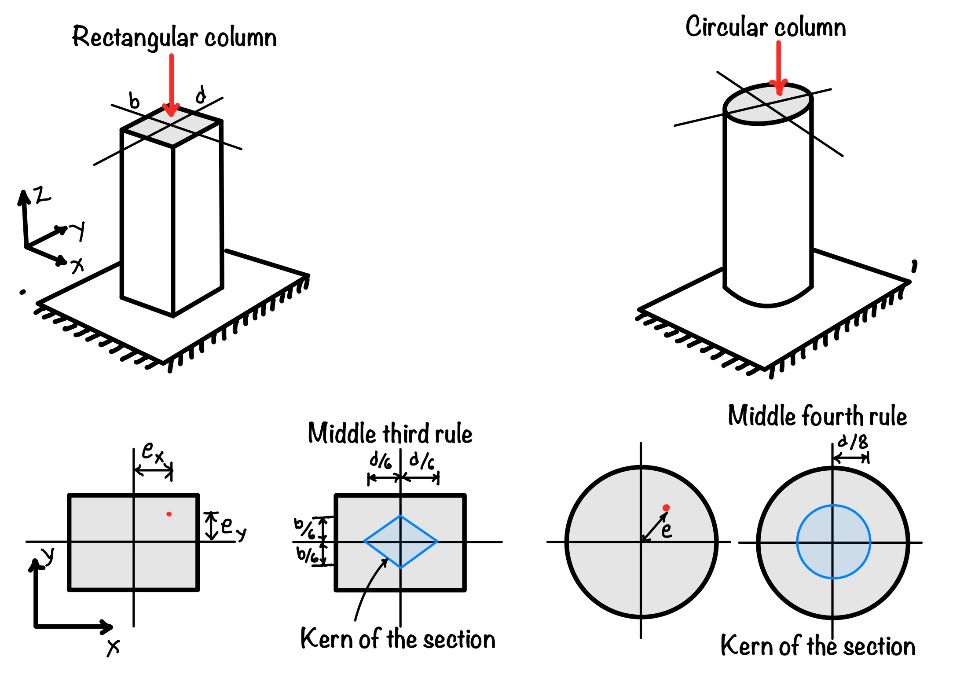
What is kern of section for rectangular column?
We have discussed the kern of the section in the above section. In this section we will find the kern of the rectangular section.
To start with lets consider the load $P$ acting in the section having the dimension $b\times d$. You can calculate the stress generated in the column due to eccentric load.
$$ \sigma = \frac{P}{A} \pm \frac{Pe_x}{Z_y} \pm\frac{Pe_y}{Z_x} $$
You can see the four corners as shown in figure and for the ease we have numbered them. So now lets find the stress in each corner.
$$ \sigma_1 = \frac{P}{A} – \frac{Pe_x}{Z_y} -\frac{Pe_y}{Z_x}\\\sigma_2 = \frac{P}{A} -\frac{Pe_x}{Z_y}+\frac{Pe_y}{Z_x}\\\sigma_3 = \frac{P}{A} + \frac{Pe_x}{Z_y} +\frac{Pe_y}{Z_x}\\\sigma_4 = \frac{P}{A} + \frac{Pe_x}{Z_y} -\frac{Pe_y}{Z_x} $$
Now you have to make sure that any of these values can not be more than zero. That means there will be no tensile stress in the column. The corner $1$ in the column is the most critical case. Hence considering that corner and applying the condition.
$$ \sigma_1 = \frac{P}{A} – \frac{Pe_x}{Z_y} -\frac{Pe_y}{Z_x} $$
You can compute the values of $Z_y$ and $Z_x$ from the geometry of the section given. Let’s compute this in detail. As a first step you must know that these are section modulus and you can write it as
$$ Z_x =\frac{ I_{xx}}{y} =\frac{bd^3/12}{d/2} = \frac{bd^2}{6} $$
Similarly you can compute for the other axis. The section modulus for the other axis is as follows:
$$ Z_y =\frac{ I_{yy}}{x} =\frac{db^3/12}{b/2} = \frac{db^2}{6} $$
In the next step you have to replace these values to the stress at corner $1$.
$$ \sigma_1= \frac{P}{bd}-\frac{6Pe_x}{db^2}-\frac{6Pe_y}{bd^2} \ge0 $$
Just solve it for the inequality.
$$ \frac{P}{bd}-\frac{6Pe_x}{db^2}-\frac{6Pe_y}{bd^2} =0\\\frac{6Pe_x}{b}+\frac{6Pe_y}{d}=1 $$
What is middle third rule?
You can recall that above relation is the equation of straight line in the intercept form which you might have seen in your school maths. Which looks like this:
$$ \frac{x}{a} + \frac{y}{b}=1 $$
You can compare these two equations to obtain the conclusion. This equation gives $a=b/6$ and $b=d/6$ . Plotting the information in the above equation you may obtain that the value of $e_x \ngtr b/6$ and the value of $e_y \ngtr d/6$.
And by closely looking the allowed eccentricity you can summarise that the it is equal to one third of the half length and width.
$$ e_x= \frac{1}{3}\bigg(\frac{b}{2}\bigg) ; e_y= \frac{1}{3}\bigg(\frac{d}{2}\bigg) $$
Hence we can say that for the rectangular section the kern of the section is middle third area of the column.
What is the middle fourth rule?
This time consider the circular column. You have to apply the same concept. The only change is the section modulus. So let’s compute the section modulus for the circular section.
$$ Z=\frac{I}{y}=\frac{\pi d^4/64}{d/2} = \frac{\pi d^3}{32} $$
You can see that the column is symmetric in cross section. Hence in this we need to consider only one axis.
$$ \frac{P}{\pi d^2/4} – \frac{Pe}{\pi d^3/32}=0 $$
Solving for $e$, we will get $e=d/8$.
$$ e=\frac{1}{4}\bigg(\frac{d}{2}\bigg) $$
Hence this is called the middle fourth rule.
Conclusion
Kern of the section is important for the column where we need no tension stress . We use this concept while making the gravity dams, retaining wall.
In this post you have learned the following key concepts:
- Kern of the section: It is the cross-section area that allows the eccentricity without producing the tension stress in the column.
- Middle third rule: Kern of the section for the rectangular column is one third of the middle of section. Hence we call it a middle third rule.
- Middle fourth rule: For columns having circular sections the kern of the section is one-fourth of the midsection.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


