Before starting the strength of the material, you need to clearly understand homogenous and isotropic material as you keep making these assumptions about the material. In this post, you will learn about homogenous and isotropic materials. Apply the concept of homogenous and isotropy symmetry in the constitutive relation.
What is homogenous material?
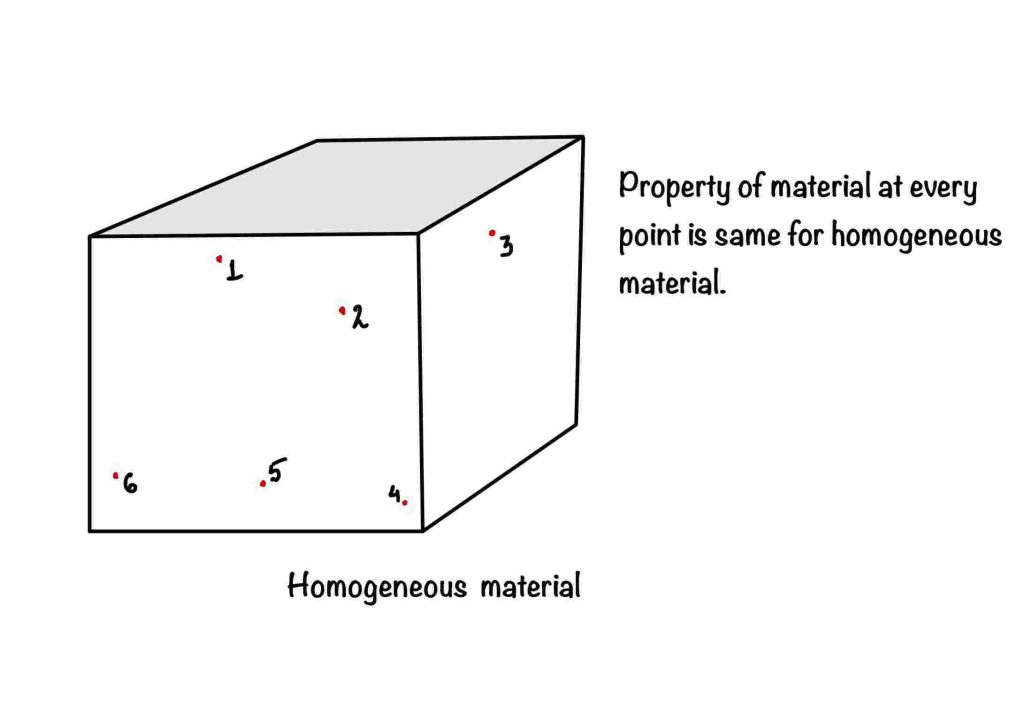
In nature, there is no homogeneity, which means nature tries to create unique things. But we want to make things homogenous to economize things. Homogenous materials have the same properties at all points. If you take a random point inside the material, all the points have the same material properties. The figure shows different points inside the material. If the material properties at every point are the same, this is called homogenous material.
What is isotropic material?
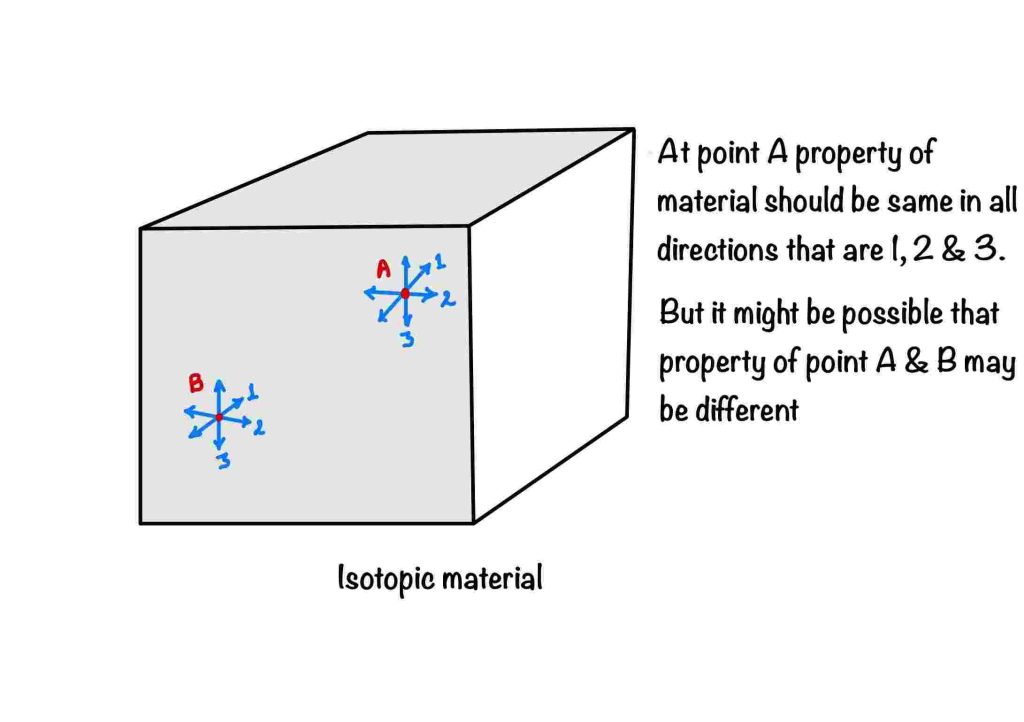
The word “isotropy” means the same in all orientations. Hence isotropic material has the same properties in all directions. If you choose any point inside the material, isotropic materials have the same properties in all directions.
What is the use of isotropy and homogeneity?
Well, to be honest, these material properties are very useful in different engineering domains while deriving fundamental relations. For example, in the strength of the material, we generally derive the pure bending theorem of the beam, pure torsion relation of the shaft, and column buckling. We assume that the material is homogenous and isotropic. Hooke’s law is also derived for the homogenous and isotropic material. We have used this assumption even in the derivation of Poisson’s ratio.
Homogenous and Isotropic in one line
To derive the fundamental relations in engineering, we need to simplify the real-life problem without changing the nature of the problem. Assuming material is homogenous and isotropic is one of the most essential assumptions which make issues simple.
In this small post, you have learned that
- Homogenous: Same property at different locations.
- Isotropic: Same property in all directions.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.