Tension members are those which are subjected to tensile force. In this article, we will focus on the determination of the tensile strength of the simplest tension member that is flats. By Indian standards, flats are denoted as ISF which means Indian standard flats.
What are tension members?
Tension members are linear members in which axial forces act to cause elongation (stretch). These type of members has a wide range of applications in buildings an other civil engineering structures. Now, let us look into the failure modes of tensile members.
This article is only applicable for plates subjected to tensile load but not for any other structural shapes (Angle sections, Channel sections)
What are the modes of failure of tension members?
Tension members can undergo three types of failure mode:
a) Design strength due to yielding of the gross section$(T_{dg})$
b) Design strength due to rupture of critical section $(T_{dn})$
c) Design strength due to block shear $(T_{db})$
Thus, design tensile strength, $T_d=\text{Min} (T_{dg},\,T_{dn},\,T_{db})$
Now let us calculate each of the design strength by taking a design example.
Step-by-step procedure using a design example
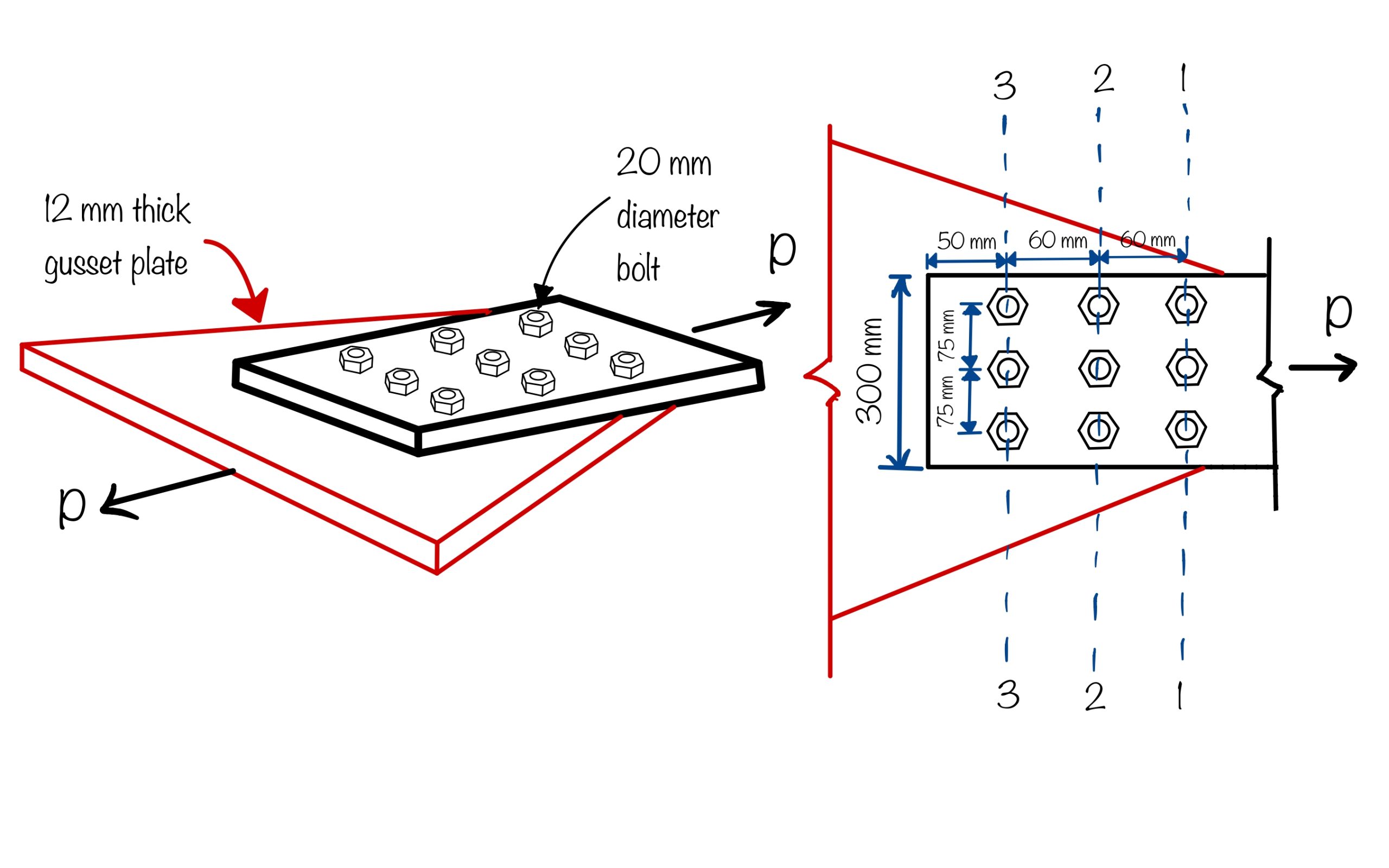
A flat plate, 300 ISF 8 mm of grade 410 is connected to a 12 mm thick gusset plate by 18 mm diameter bolts of grade 4.6. Calculate the design tensile strength of the member. The bolting pattern is shown below.
How to calculate design tensile strength due to yielding of the gross section $(T_{dg})$
As per IS 800:2007, the design strength of member governed by $T_{dg}$ is given as:
$$ T_{dg}=A_gf_y/\gamma_{m0} $$
where,
$f_y=$ yield stress of the material
$A_g=$ gross area of cross-section
$\gamma_{m0}=$ partial safety factor for failure in tension by yielding (Table 5, IS 800:2007)
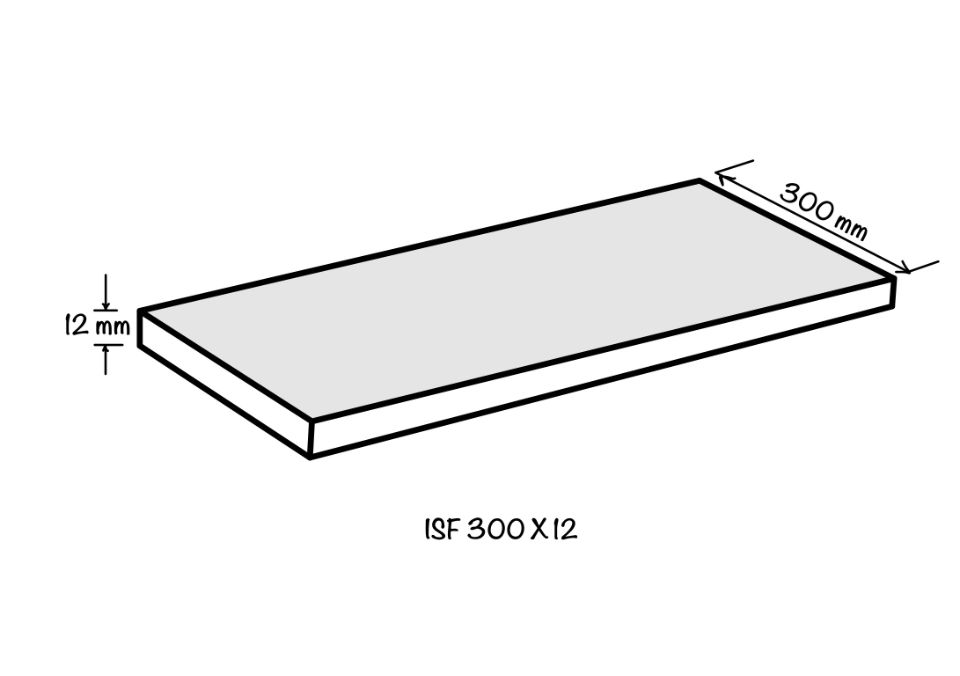
In the current design example, for 300 ISF 8 mm we have,
Width of the plate, $b=300\; mm$
Thickness of the plate, $t=8 \; mm$
Hence, $A_g=b\times t = 300 \times 8 = 2400 \; mm^2$
Therefore,
$$ T_{dg}=A_gf_y/\gamma_{m0}=2400\times 250/1.1 = 545.45 \; kN $$
How to calculate design strength due to rupture of the critical section $(T_{dn})$
As per IS 800:2007, the design strength of member as governed by $T_{dn}$ is given as:
$$ T_{dn}=0.9A_nf_u/\gamma_{m1} $$
where,
$f_y=$ Ultimate stress of the material
$A_g=$Net effective area of cross-section
$\gamma_{m0}=$ partial safety factor for failure at ultimate stress (Table 5, IS 800:2007)
How to calculate the net section area, $A_n$?
The net effective area, $A_n$ of a cross-section is basically the expected path of rupture of the plate when subjected to tensile load. Thus, it will fail through the bolt-hole path (staggered or linear) for the lowest effective net cross-section area.
IS 800:2007 defines net section area for flat plates as:
$$ A_n=[b-nd_h+\Sigma\frac{p_{si}^2}{4g_i}]t $$
where,
$b, t=$ width and thickness of the plate respectively,
$d_h=$ diameter of the bolt hole
$g=$ gauge length between bolt holes (centre-to-centre distance of the bolt measured perpendicular to the direction of applied load)
$p_s=$ staggered pitch length between bolt holes, as shown in figure below.
$n=$ number of bolt holes in the critical section
$i=$ subscript for summation of all the inclined legs
Note: Here, the term $\frac{p_{si}^2}{4g_i}$ is used only for staggered type bolting pattern.
In the given example, the bolting pattern is chain type for which the critical section will be governed by:
$$ A_n=[b-nd_h]t $$
Here,
$b=300\; mm$
$n=3$ $d_h=22\; mm$ i.e. $20+2=22\; mm$ as per Clause 6.3.1 IS 800:2007
$t=8\; mm$
Hence, $A_n=[b-nd_h]t=[300-3\times22]\times8=1872\; mm^2$
Now, $T_{dn}=0.9A_nf_u/\gamma_{m1}=0.9\times 1872\times 410/1.25=552.6 \; kN$
How to calculate design strength due to block shear $(T_{dg})$
As per IS 800:2007, the design strength of member governed by $T_{dg}$ is given as:
$$ T_{db}=\text{Min}(T_{db_1},T_{db_2}) $$
How to calculate the $T_{db_1}$ and $T_{db_2}$ we will see in the next step
$$ T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}} $$
Now we will see the calculation of $T_{db_2}
$$ T_{db_2}=\frac{0.9A_{vn}f_u}{\sqrt{3}\gamma_{m1}}+\frac{A_{tg}f_y}{\gamma_{m0}} $$
where,
$f_y=$ yield stress of the material
$f_y=$ ultimate stress of the material
$A_{vg}, A_{vn}=$ minimum gross and net area in shear along bolt line parallel to external force respectively (refer to figure shown below)
$A_{tg}, A_{tn}=$ minimum gross and net area in tension from the bolt hole to the end bolt line (to toe end in case of angle), perpendicular to the line of force (refer to figure shown below)
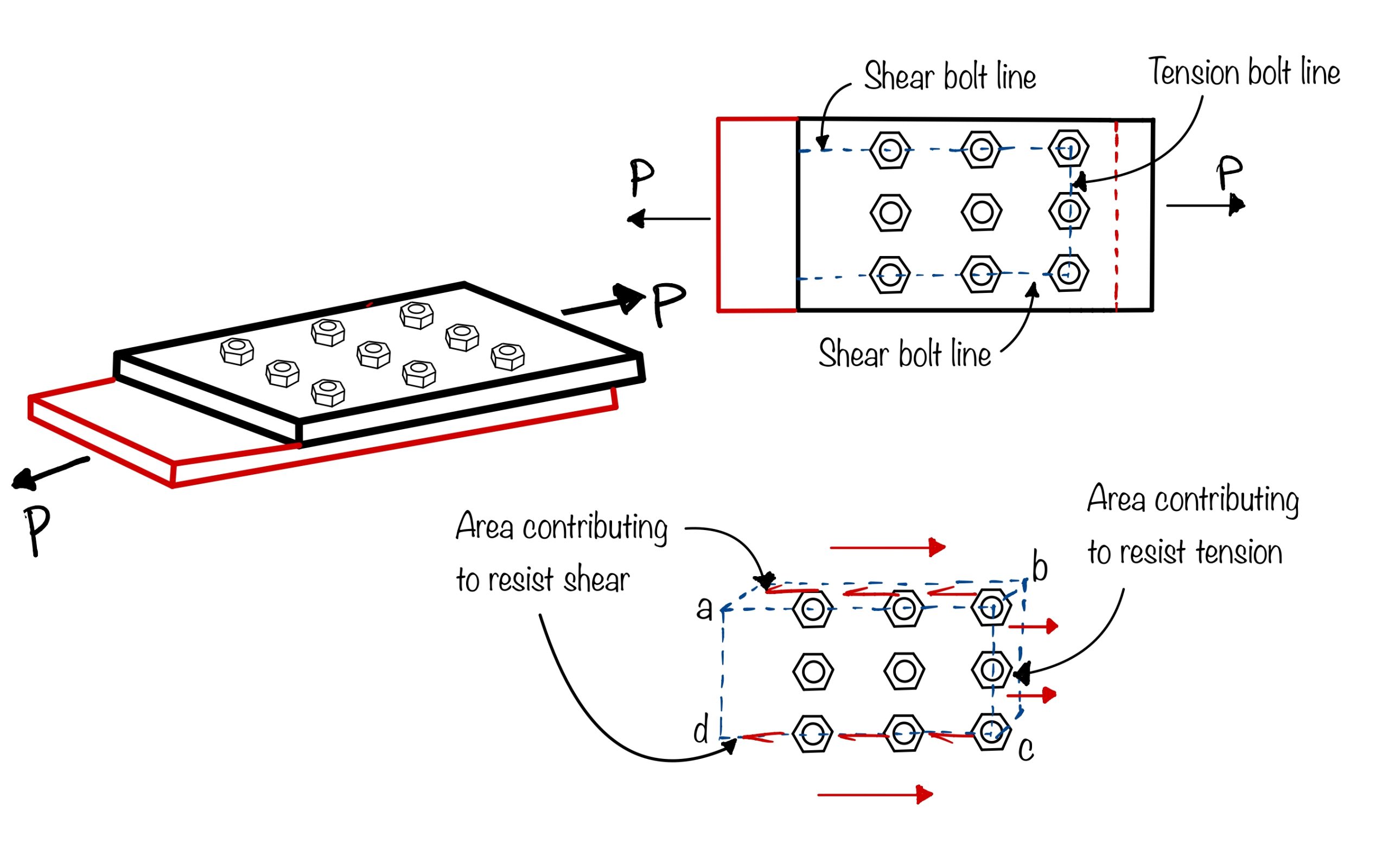
Step a: Determine the shear bolt line and tension bolt line
Refer to figure below on simple tricks to determine the shear and tension bolt lines. Clause 6.4.1 of IS 800:2007 defines the same in detail.
Step b: Calculate $A_{vg}, \; A_{vn}, \; A_{tg}, \; A_{tn}$ for the given problem
In the given problem,
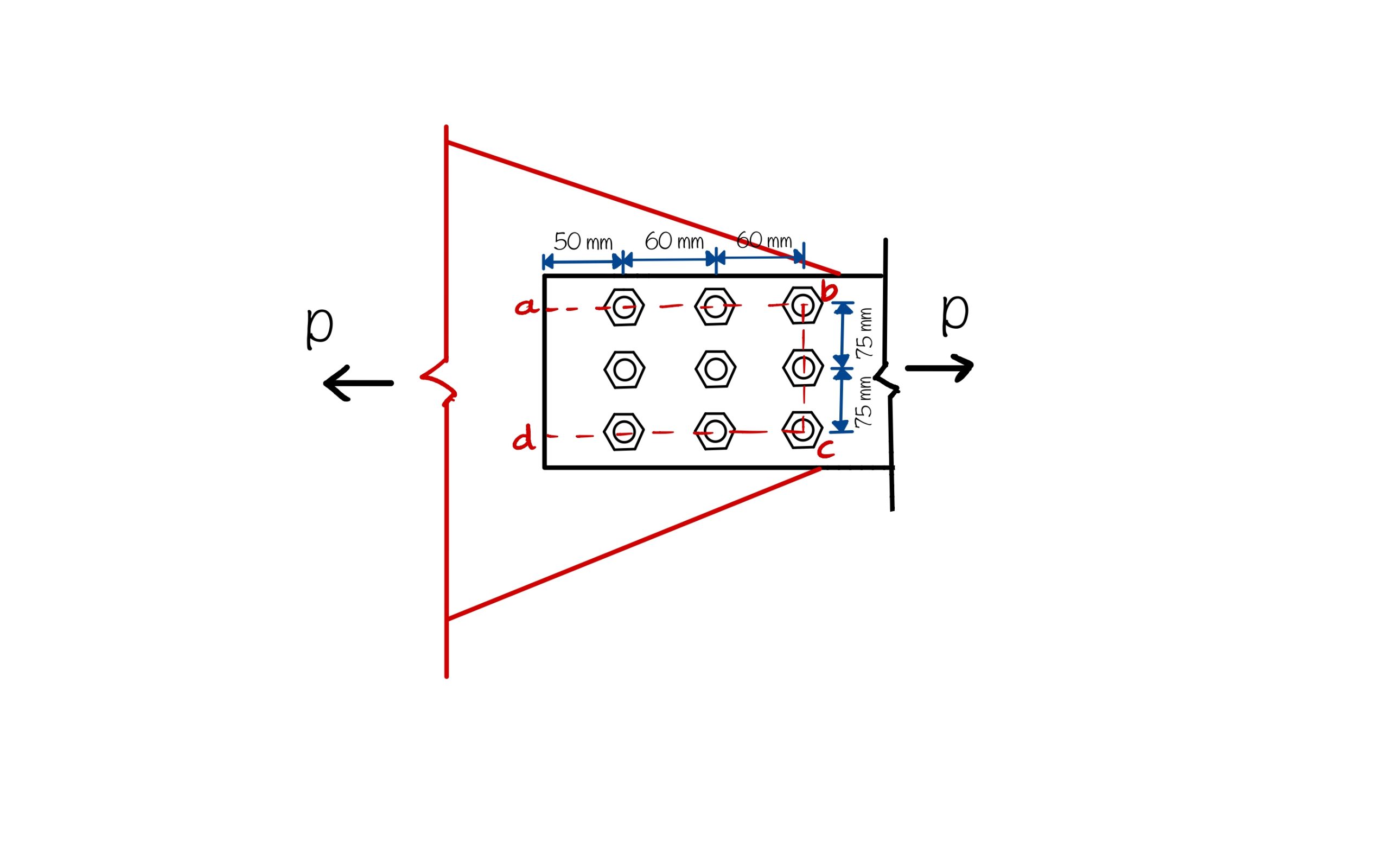
$A_{vg}=$ Gross area along $ab$ and $cd$ $=2\times[(50+60+60)\times8]=2720\; mm^2$
$A_{vn}=$ Net area along $ab$ and $cd$ $= 2\times[(50+60+60-2.5\times22)\times8]=1840\; mm^2$
$A_{tg}=$ Gross area along $bc$ $=(75+75)\times8=1200\; mm^2$
$A_{tn}=$ Net area along $bc$ $=(75+75-2\times22)\times8=848\; mm^2$
Therefore,
$$ T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}} $$
Now putting the values in the formula
$$ T_{db_1}=\frac{2720\times250}{\sqrt{3}\times1.10}+\frac{0.9\times848\times410}{1.25}= 607.24 \; kN $$
After calculating the $T_{db_1}$ now move to the $T_{db_2}$
$$ T_{db_2}=\frac{0.9A_{vn}f_u}{\sqrt{3}\gamma_{m1}}+\frac{A_{tg}f_y}{\gamma_{m0}} $$
$$ T_{db_2}=\frac{0.9\times1840\times410}{\sqrt{3}\times1.25}+\frac{1200\times250}{1.10}=586.33\; kN $$
Hence, $T_{db}=586.33\; kN$
Thus, design tensile strength, $T_d=\text{Min} (T_{dg},\,T_{dn},\,T_{db})= T_{dg}=545.45 \; kN$
Conclusions
In this article, we have seen how to obtain the tensile strength of a flat plate with a chain bolting pattern with a design example.
A few learning points are:
- Failure modes: Tension member can fail in three modes: Yielding, Net-section rupture, and Block shear failure
- Strength: Determination of net section area, $A_n$ is an important step in design strength calculation.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


