Isentropic processes are thermodynamic processes in which the entropy of a fluid remains constant. Real systems that typically use this process as an idealization include the turbine and compressor stages in power plants and air conditioning systems.
An essential indicator of the effectiveness of these systems is their isentropic efficiency, which is calculated as the ratio of the actual work to the ideal work done. Engineers are constantly seeking ways to increase isentropic efficiency for these systems to operate more effectively and use less energy.
As it aids in understanding actual thermodynamic systems and improves their functionality, the idea of an isentropic process plays a significant role in practical engineering.
Definition of Isentropic process
An isentropic process is a thermodynamic process in which the entropy of a fluid remains constant. Mathematically, this can be expressed as
$$dS = 0$$
, where $S$ is the entropy of the fluid. The process is a straight line in a TS diagram, as shown below.
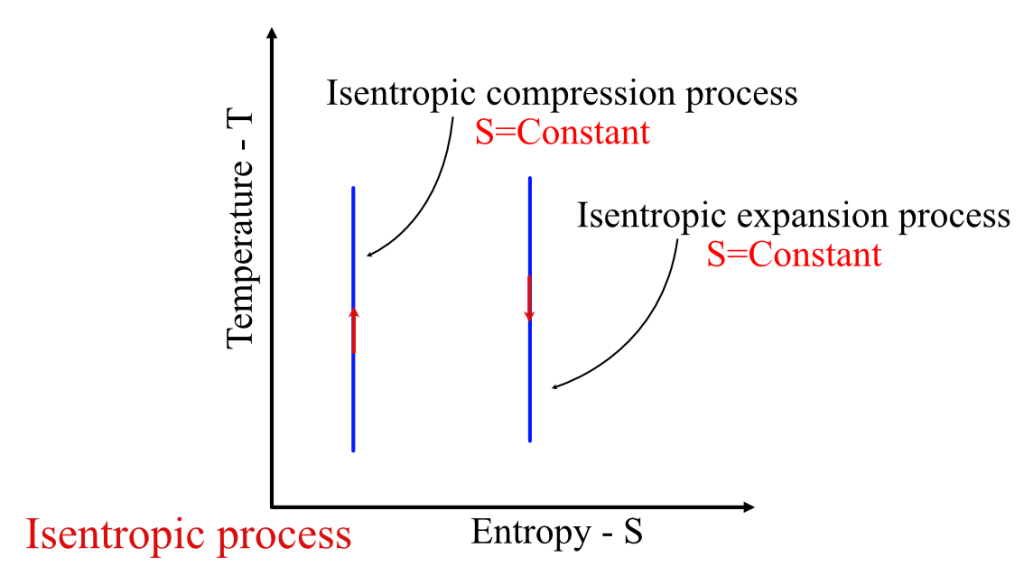
Isentropic processes can also be represented using the first and second laws of thermodynamics. The first law of thermodynamics states that energy is conserved, and for an isentropic process, this can be expressed as $dU = dQ – dW$, where U is the internal energy of the fluid, Q is the heat added to the fluid, and W is the work done on or by the fluid. The second law of thermodynamics states that entropy is a measure of disorder, and for an isentropic process, this can be expressed as
$$dS = dQ/T$$, where T is the temperature of the fluid.
Additionally, for an isentropic process, the ratio of the specific heats (Cp/Cv) is constant, and the temperature and pressure in the fluid change in proportion to each other as well. This becomes
$P*V^(\gamma) = \text{Constant}$
where $\gamma$ = Cp/Cv and P is pressure and V is volume.
The above relation can be expressed in different forms for an ideal gas as below:
$$TV^{\gamma -1} = \text{Constant} $$
In practice, real-world systems rarely undergo truly isentropic processes, but the concept is used as an idealization for analyzing many systems, including compressor and turbine stages in power plants and air conditioning systems. The difference between the actual performance and the ideal isentropic performance is often used as a measure of the system’s efficiency.
Work done for ideal gas
The work done by an ideal gas during an isentropic process can be derived using the first law of thermodynamics and the ideal gas law.
For an isentropic process, the change in internal energy of an ideal gas is zero (dU = 0) since the entropy of the system is constant, and no heat is transferred in or out of the system (dQ = 0). So we can express the work done by the system as: dW = -dU
Using the ideal gas law PV = nRT, where P is pressure, V is volume, n is the number of moles, R is the gas constant and T is temperature, we can express the work done by the system as
$$ dW = -nRdT$$
However, since the process is adiabatic, there is no heat exchange with the environment, and the temperature change within the gas can be described as dT = -(T/V)dV
Therefore, we can substitute the above expression in the work equation dW = -nRT(dV/V)
Since PV^(gamma)=constant where gamma = Cp/Cv, and Cp/Cv = γ, we can substitute this in the above equation and express it as
dW = -(P*V^(gamma-1))dV
It is worth noting that the above derivation for the work done assumes that the process is reversible. In practice, the processes are almost never reversible, the isentropic process is just an approximation to the real processes that occur in the systems.
Isentropic efficiency
In practical engineering applications, most of the steady flow devices aren’t reversible in nature. Thus, even though they are adiabatic in nature, they aren’t isentropic (i.e., adiabatic and reversible). That deviation of the actual engineering devices from that of an ideal isentropic one is defined using the concepts of isentropic efficiencies.
Consider the figure below, which shows the plot of a real compression process and an isentropic compression process in a TS diagram. Here, you can see that, despite having the same pressure ratio, the gas has higher energy (enthalpy) when compressed in the real compression process. This variation of the energy from the ideal isentropic process is accounted for with the help of isentropic efficiencies.
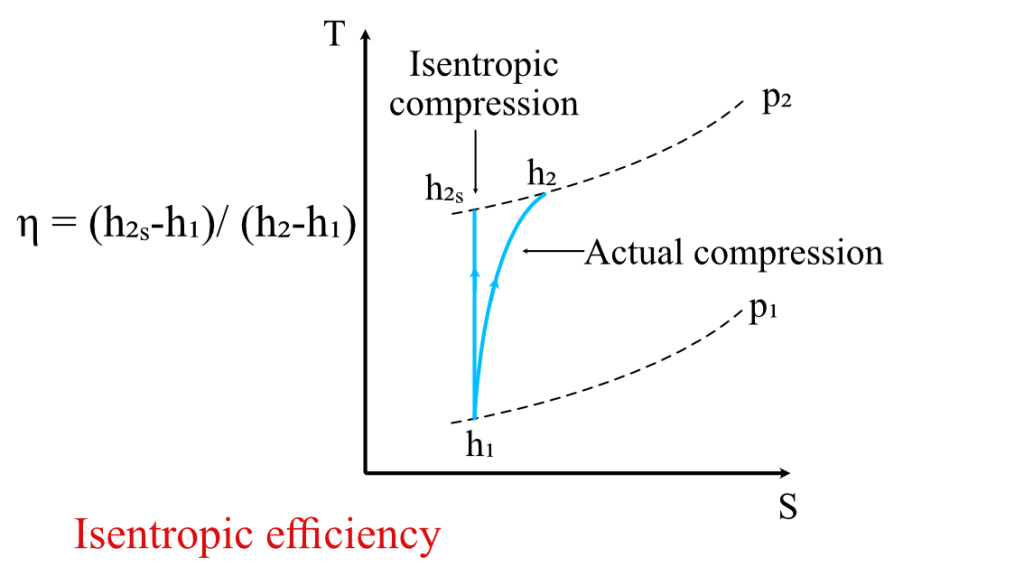
In the case of the isentropic processes, efficiency defines the ratio of the work done by the device to the work done when operated under ideal isentropic conditions. The formula for the isentropic efficiency is different for the turbine, compressors, and nozzles.
Like, as for the turbines, the isentropic efficiency is
$$ \eta_T = \frac{\text{Actual Turbine work}}{\text{Isentropic Turbine work}} $$
whereas the equation for the compressors is just inverse
$$ \eta_C = \frac{\text{Isentropic Compressor work}}{\text{Actual Compressor work}} $$
In general, these values range from 70% to 90%.
Practical examples
Well, just like any thermodynamic process, the applications of this process can also be found in your home. Whether it’s the compressor of your refrigerator or air-conditioner, the working principle is an isentropic process.
Here are some practical engineering examples of isentropic processes:
- Compressor and turbine stages in power plants: The isentropic efficiency of these stages, which is the ratio of the actual work done to the maximum possible work, is an important measure of the performance of the power plant. Engineers aim to increase the isentropic efficiency of these stages in order to improve the overall performance and energy efficiency of the power plant.
- Gas turbine engines: The turbine in a gas turbine engine is often modeled as an isentropic process, as it expands a high-pressure, high-temperature gas to produce work. The isentropic efficiency of the turbine is an important measure of the engine’s performance.
- Air conditioning systems: The compressor in an air conditioning system is often modeled as an isentropic process, as it compresses a low-pressure, low-temperature refrigerant to a high-pressure, high-temperature state. The isentropic efficiency of the compressor is an important measure of the system’s performance.
- Fluid mechanics: In fluid mechanics, the fluid flow can be considered isentropic when the fluid behaves like an ideal gas, and the process is adiabatic, and no heat is transferred between the fluid and the environment.
- Rockets: In rocket propulsion systems, the isentropic flow is considered an idealization to model the behavior of the high-speed nozzle flow, for example, in the nozzle of a rocket engine.
Overall, the isentropic process is a widely used concept in practical engineering that helps to understand and improve the performance of thermodynamic systems such as power plants, gas turbine engines, air conditioning systems, and fluid and rocket propulsion systems.
Conclusions
In summary, an isentropic process is a thermodynamic process in which the entropy of a fluid remains constant. It is frequently employed in real-world engineering as an idealization for a variety of systems, including air conditioning systems, gas turbine engines, and the compressor and turbine stages in power plants. An essential indicator of how well these systems perform is isentropic efficiency, which is the ratio of the work that is actually completed to the maximum that may be accomplished.
Important takeaways from the discussion above include:
- Definition: The isentropic process is a thermodynamic process in which the entropy of a fluid remains constant.
- Formulation: Isentropic process can be represented mathematically as dS = 0, and the ratio of specific heat Cp/Cv is constant for this process.
- Engineering Applications: The isentropic process is an idealization for analyzing real systems such as power plants, gas turbine engines, air conditioning systems, and fluid and rocket propulsion systems.
- Isentropic efficiency: The isentropic efficiency, which is the ratio of actual work done to the maximum possible, is an important measure of the performance of these systems.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


