Stress is required to design the structure. The safety of the structure is assured by this. We will discuss in this blog how we can measure the it in the structure. So let’s start with defining the simple stress.
In this blog, we will discuss what is stress. Before defining the it, you must feel this. If you apply the force to the calk stick as shown in the figure and keep on increasing the load, it will break after some time. This is happening due to stress.
Definition of the simple stress
Simple stress can be defined as the force per unit area. (This definition is very crude and in an average sense.)
$$\underbrace\sigma_{(\text{Sigma})}= \frac{P}{A}$$
Where:
- $\sigma$ is the stress and pronounced as (sigma),
- $P$ is the force (It is the average force in the cross-section)
- $A$ is the area of the cross-section.
It depends on the direction of force and also on the orientation of the plane. Therefore fore we say it is the tensor quantity and to be precise stress is the second-order tensor.
Limitations in the simple stress formula
Limitations of the formula discussed above:
- Average sense: The stress that we have defined here is average stress, which means it may be possible that at some point in the cross-section, the stress value may exceed.
- Homogenous and Isotropic: We have assumed that the material is homogenous and isotropic in nature.
Interaction with stress
To understand how stress is the second order tensor or rather we can say how it depends on the orientation of the plane, we will play with this widget.
From this widget you can easily understand that the stress will depend on angle theta also, apart from the load and area. For the same values of load and area, you will find the different stress.
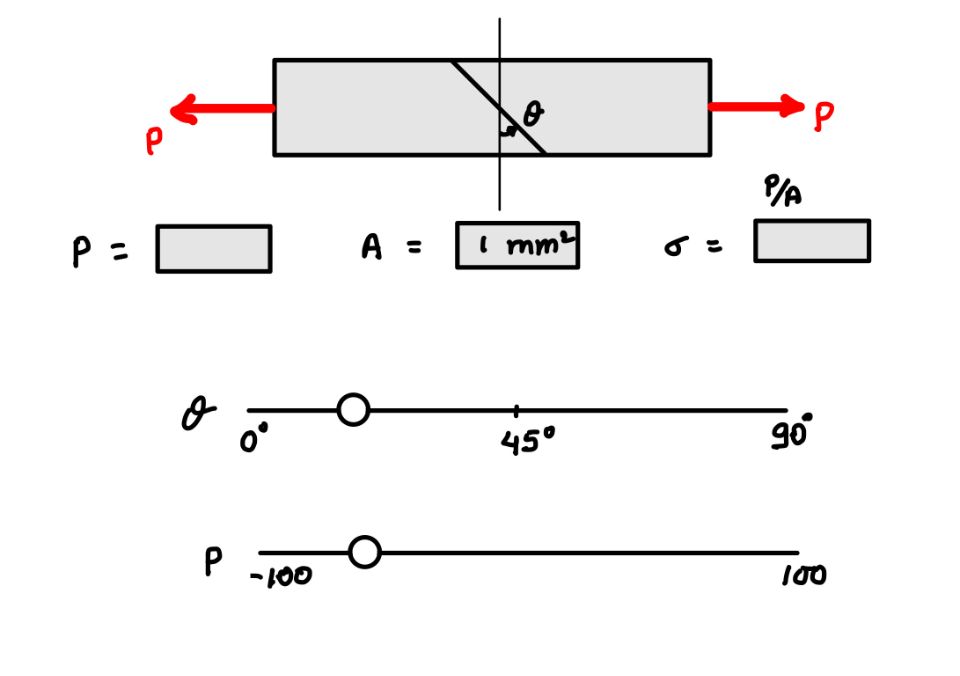
Application
Stress is important for the design of structures. The information about the stress at any point is useful to assure the design safety of that member.
Stress at a point
The definition of stress which we have used here is in the average sense. That means it assumes that the stress due to any load $P$ is uniformly distributed throughout the cross-section, which may not be true in the practical situation.
Hence to be more precise in the definition of stress we can define it as ” It is the intensity of internal resistance at the vicinity of the point.” For detailed discussion of stress in this regard you may refer to the article stress at a point. In this article you will find the advance concept and practical application of stress.
Conclusion
Simple stress is the internal resistance of the body. You always keep this thing in mind while reading the article.
In this blog, you have learned the following things:
- Simple stress: In this article, we have discussed how stress at a point is different than simple stress. Simple stress is more of an average sense.
- Stress is second order tensor quantity: As you have seen in the widget when you change the angle of the cross-section the stress values change. Hence stress also depends on the direction of the area.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


