Mechanics is the science of forces and motions. The origins of mechanics could be traced back to 4th century BC when Aristotle founds the system of Aristotelian physics, but it was not until 1687 when Isaac Newton publishes his three laws of motion that laid the foundation for what is now known as classical mechanics.
Continuum mechanics is a branch of mechanics that is a combination of mathematics and physical laws that approximate the large−scale behavior of materials modeled as a continuous mass rather than as discrete particles matter that is subjected to mechanical loading. Modeling an object as a continuum assumes that the substance of the object completely fills the space it occupies and is free from any discontinuity or voids.
Solid mechanics is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of external or internal forces for the purpose of designing structure better. I think so that it is essential for the reader to know at the start itself about the basics. During the elementary physics, we have learned about force. The force causes a change in the state of a body. It either displaces the body or deforms the body. We would be dealing with the latter condition since rigid body movement is beyond the scope of this series.
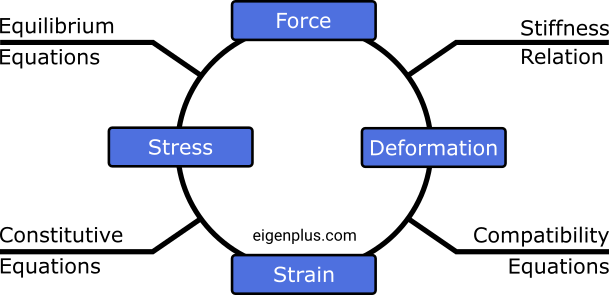
A material has a rest shape and its shape departs away from the rest shape on the application of external Force. The amount of departure from rest shape is called Deformation. Force and deformation are related together by stiffness relation. The proportion of deformation to original size is called Strain. Deformation and Strain are related together by Compatibility equations. The material tries to resist this deformation and produces internal resistance which is termed as Stress. Stress and strain are related together by Constitutive Equations. If the material body is under equilibrium then the internal force (Stress X cross−sectional area) generated is equal to the applied external force. And, thus the external force and internal stress are related by equilibrium equations.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.