To understand what stress transformation is and why it is needed, let’s perform a demonstration. Take a piece of chalk and try to twist it from both ends, as shown in the figure. Twist the chalk until it breaks. You can observe the failure surface at a $45^\circ$ angle, even though you are applying a twist that creates the pure shear in the plane normal to the axis. This phenomenon happens because of the transformation of stress.
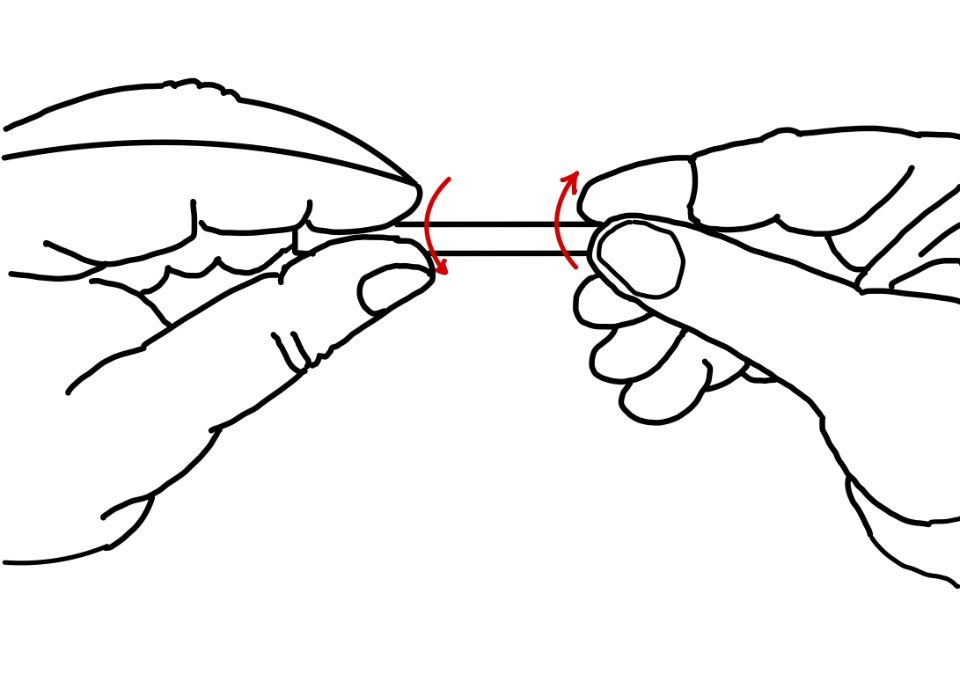
To comprehend how pure twisting leads to chalk failure in tension, we need to examine the transformation from shear to tensile stress. This process is critical because it determines the maximum allowable stress or ultimate tensile strength, which is the point at which the material fractures. Therefore, it’s essential to understand the stress-strain relationship of the material to identify this critical point. By doing so, we can determine the maximum stress the material can withstand before it fails in tension. In summary, understanding the transformation from shear to tensile stress and the maximum allowable stress is crucial to comprehend how pure twisting causes chalk to fail in tension.
Why Do We Need a transformation of stress?
We need the maximum stress value at a point to design a structure. Hence, these maximum stresses may be different for different types of materials. For brittle materials, we are looking for the maximum tensile stress.
From our previous discussion on stress, you know that stress is a tensor quantity, and the value of stress varies with the change in the direction of the plane. It may be possible that the maximum stress occurs at a different orientation from the current state of stress.
To define the state of stress at a point in 2D, you need four components; in 3D, you need nine.
$$ \sigma= \begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \tau_{xy} & \sigma_{yy} \end{bmatrix} $$
$$ \sigma= \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{bmatrix} $$
What Is the equation for the transformation of stress?
To derive the stress transformation, let’s consider the positive state of stress in two dimensions. It is the stress block of unit depth. In the front, the square is named $ABCD$.
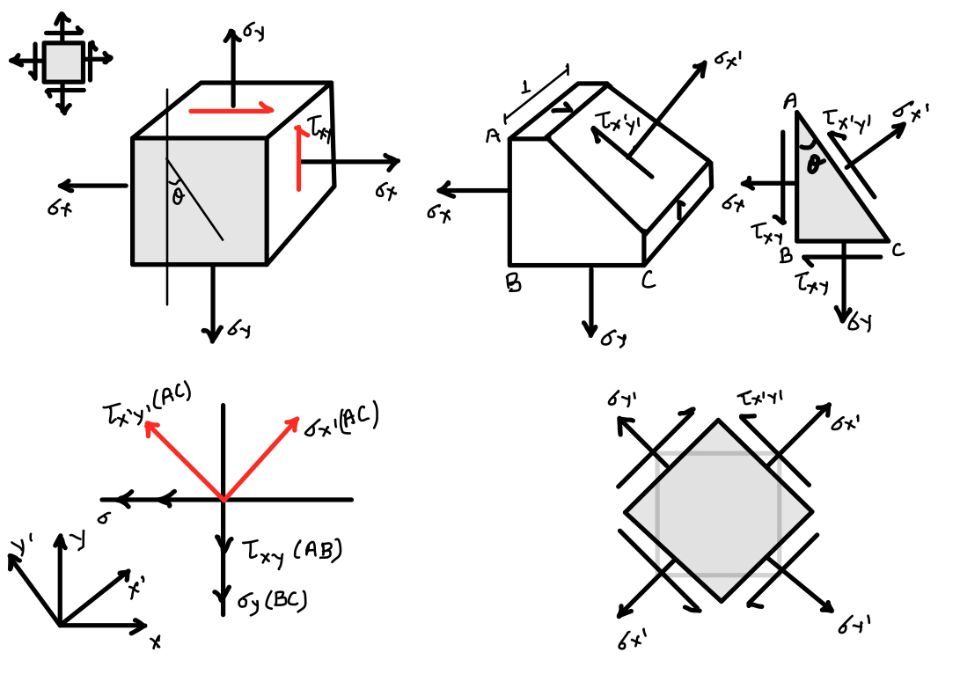
If you want the state of stress at a point in the new coordinate system $X’Y’$, part (b) of the figure shows the 3D view of the stress block. The stress in the $XY$ coordinate system is $\sigma_x$, $\sigma_y$, $\tau_{xy}$. The sign of positive and negative shear stress is discussed in more detail in a separate post. For the time being, you can consider the stress in the positive direction in the positive plane as positive.
You can refer to part 3 of the figure. It will show you the stress and the area in which they are acting. It also shows how these forces are now being balanced.
You can write the equation of equilibrium in the $X’$ direction.
$$ \sigma_{x’}=\sigma_x AB \cos {\theta}+\sigma_y BC \sin {\theta}+\tau_{xy}BC \cos{\theta}+\tau_{xy}AB\sin{\theta}\\ \tau_{x’y’} =-\sigma_x AB \sin {\theta} +\sigma_y BC\cos {\theta}-\tau_{xy}AB \sin {\theta}+\tau_{xy}BC\cos {\theta} $$
You can refer to part 4 of the figure. Here you can find the triangle with angle $\theta$. $\cos{\theta}$ = $AB/AC$, and $\sin\theta$ = $BC/AC$. Now putting these values in the above equation.
$$ \sigma_{x’}=\sigma_x \frac{AB}{AC} \cos {\theta}+\sigma_y \frac{BC}{AC} \sin {\theta}+\tau_{xy}\frac{BC}{AC} \cos{\theta}+\tau_{xy}\frac{AB}{AC}\sin{\theta}\\\tau_{x’y’} =-\sigma_x \frac{AB}{AC} \sin {\theta} +\sigma_y \frac{BC}{AC}\cos {\theta}-\tau_{xy}\frac{BC}{AC} \sin {\theta}+\tau_{xy}\frac{AB}{AC}\cos {\theta} $$
After this
$$ \sigma_{x’}=\sigma_x \cos^2 {\theta}+\sigma_y \sin^2 {\theta}+\tau_{xy}\sin \theta\cos{\theta}+\tau_{xy}\cos\theta\sin{\theta}$$
$$ \tau_{x’y’}=-\sigma_x \sin{\theta}\cos {\theta}+\sigma_y \cos {\theta}\sin {\theta}-\tau_{xy}\sin^2{\theta}+\tau_{xy}\cos^2{\theta}$$
$$\sigma_{x’}=\sigma_x \underbrace{\cos^2 {\theta}}_{\frac{1+\cos2\theta}{2}}+\sigma_y \underbrace{\sin^2 {\theta}}_{\frac{1-\cos2\theta}{2}}+\tau_{xy}\underbrace{2\sin \theta\cos{\theta}}_{\sin2\theta}$$
$$ \tau_{x’y’}=-\frac{\sigma_x -\sigma_y}{2}\underbrace{2\sin \theta\cos{\theta}}_{\sin2\theta}-\tau_{xy}\underbrace{\sin^2 {\theta}}_{\frac{1-\cos2\theta}{2}}+\tau_{xy} \underbrace{\cos^2 {\theta}}_{\frac{1+\cos2\theta}{2}}$$
Substituting the above values in the equation using the half-angle formula from trigonometry, you can finally write the equation in the following form.
$$ \sigma_{x’} = \frac{\sigma_x+\sigma_y}{2}+\frac{\sigma_x – \sigma_y}{2}\cos{2\theta}+\tau_{xy}\sin{2\theta} $$
$$ \tau_{x’y’} = -\frac{\sigma_x – \sigma_y}{2}\sin{2\theta}+\tau_{xy}\cos{2\theta} $$
The above equation gives the stress values in the new axes.
What Do We Mean by Principal Stress and Principal Plane?
When the normal stress at the point is maximum, that maximum normal stress is the principal stress, and the plane on which this principal stress is acting is called the principal plane.
To find out the angle of the principal plane, we need to differentiate the normal stress with respect to $\theta$. So let’s perform the differentiation of the normal stress.
$$ \frac{d\sigma_{x’}}{d\theta}= -\frac{\sigma_x – \sigma_y}{2}2\sin{2\theta}+\tau_{xy}2\cos{2\theta} = 0 \\\frac{\sigma_x – \sigma_y}{2}\sin{2\theta}=\tau_{xy}2\cos{2\theta} \\ $$
From this, we can find the value of the angle of principal stress.
$$ \tan 2\theta_1 =\pm \frac{\tau_{xy}}{\frac{\sigma_x-\sigma_y}{2}} $$
Why Do Cracks Occur at $45^\circ$ in Beams?
To illustrate the concept of stress in a practical scenario, let’s consider a simply supported beam that is subjected to a uniformly distributed load, as shown in part (a) of the figure. To understand the state of stress at different points in the beam, let’s focus on three specific points, namely $A$, $B$, and $C$. So let’s draw the state of stress in the same coordinate in which the beam is lying.
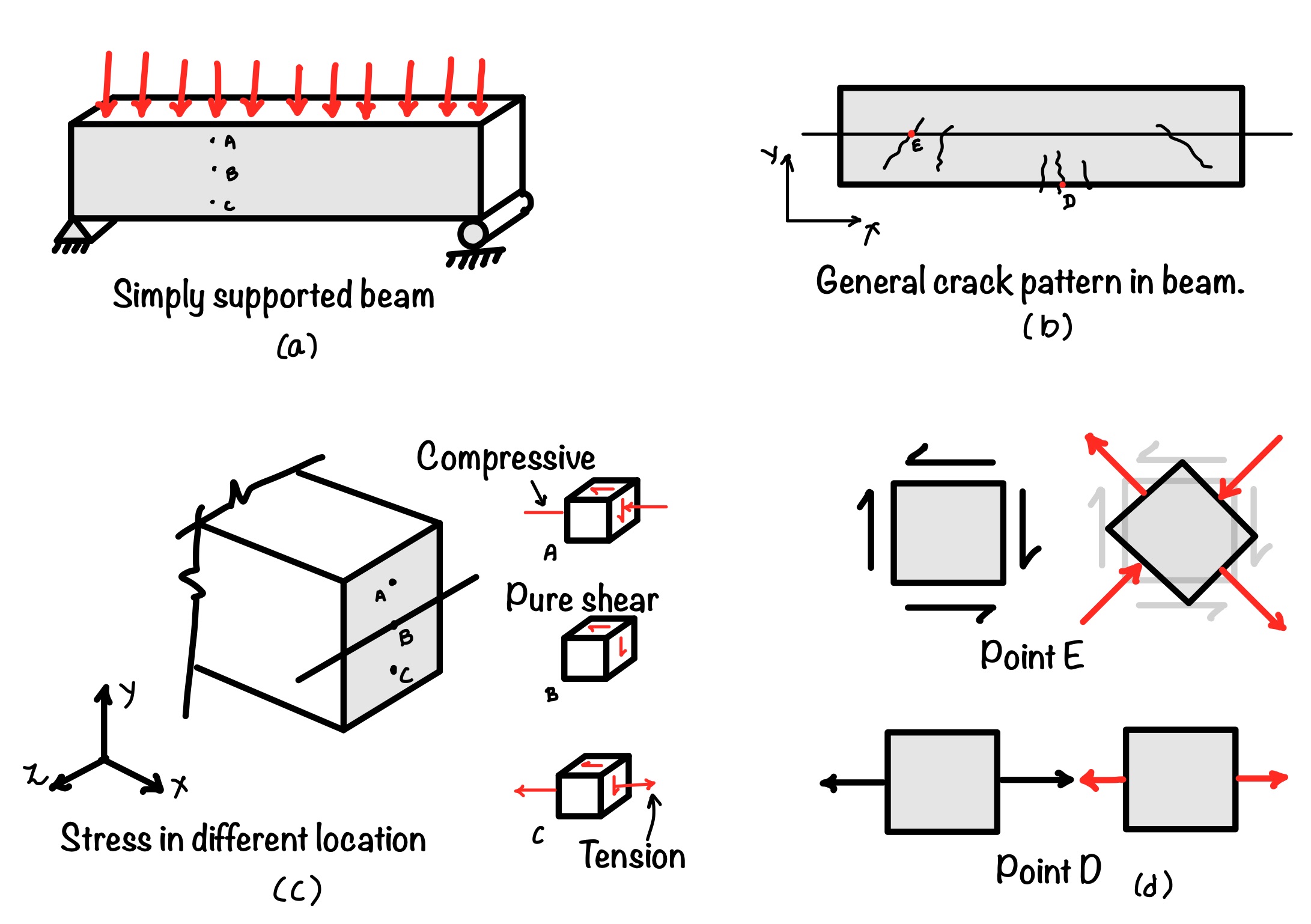
Now consider point $A$. It is in the upper part of the beam; hence, it will have compression and shear stress. At point $B$, only shear stress is acting that is pure shear stress condition. The point $C$ in the lower portion of the beam has tension and shear stress conditions, as shown in the figure. You can see in the part (b) of the figure two points we have considered. The point $E$ is at the pure shear condition, in this condition the tensile stress occurs at the $45^{\circ}$. As the concrete is brittle material so weak in tension, hence failure occurs at this plane.
Why Does a Mild Steel Tensile Specimen Have a Cup Cone Fracture at Failure?
As you know, mild steel is a ductile material, and ductile materials fail in shear. When you apply tensile stress to mild steel, the stress condition is shown in the figure.
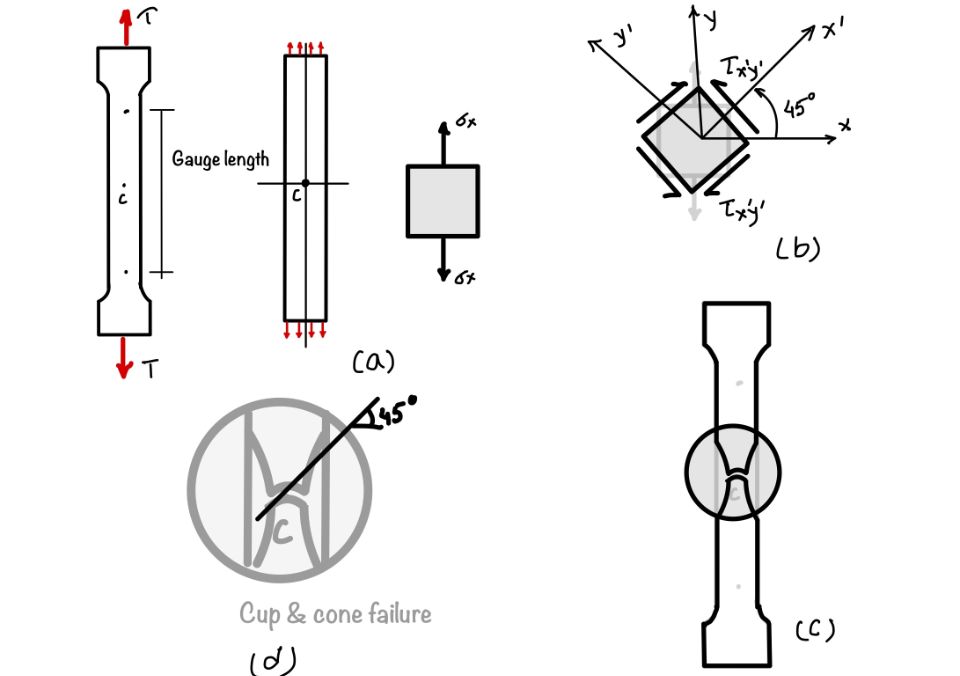
The stress is tension in the $y$ direction, and there are no other stress in the point. This state of stress is shown in part (c) of the figure. In this case, the maximum shear stress occurs at an angle of $45^\circ$. Hence, this is the reason why mild steel fails at $45^\circ$ by forming the cup and cone failure.
Why Does Chalk Break at $45^\circ$ When Subjected to Twist?
Chalk is a brittle material and weak in tension. When we apply a twist to the chalk, as shown in the figure, pure shear stress is applied to the chalk. Hence, the maximum torsion stress occurs in the chalk at the middle of the chalk.
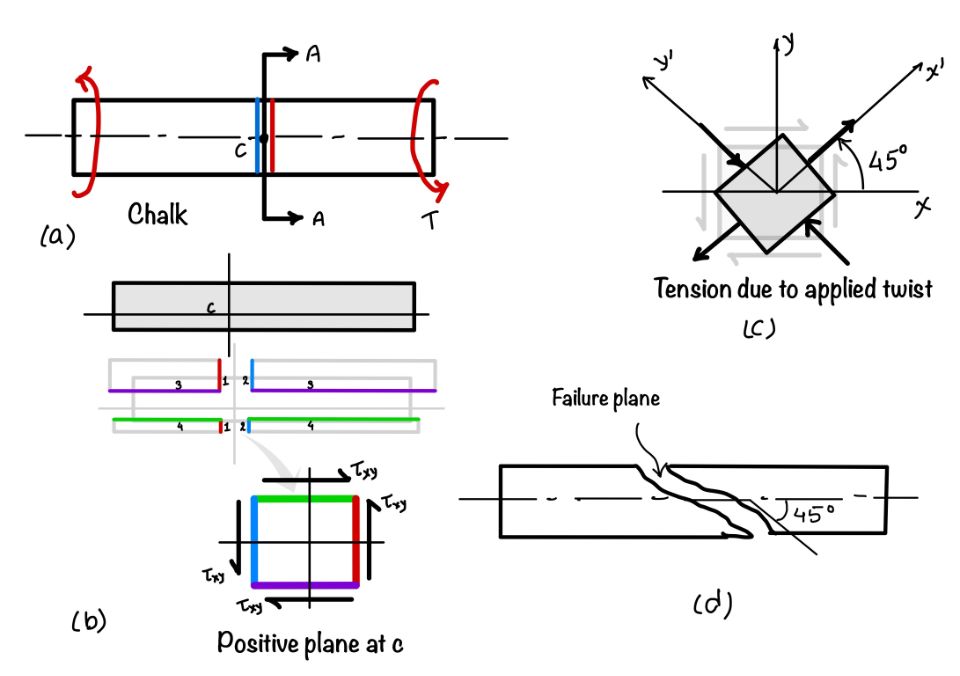
Applying the transformation to the midpoint in the chalk, we can realize that the maximum tensile stress in the material occurs at an angle of $45^\circ$ from the $x$ axis.
So, this is the reason why chalk breaks at an angle of $45^\circ$ to the $x$ axis.
Conclusion
In this post, you have learned the requirement of stress transformation and the different cases that we have explained with the help of stress transformation. Another way of doing this is Mohr’s circle. It is easier and visually more appealing than the stress transformation.
You have learned the following key concepts in this article:
- Stress: Stress is a tensor quantity. To represent the state of stress at a point, we need four stress components in 2D and nine stress components in 3D conditions.
- Principal plane: The plane where the normal stress at a point becomes maximum is called the principal plane. And this maximum normal stress is the principal stress.
- Failure: Failure of any member depends on the strength of that material. And the strength of that member depends on the material properties of the member.
- Cup and Cone failure: This type of failure occurs in mild steel because it is weak in the shear as it is a ductile material. The maximum shear stress occurs at an angle of $45^\circ$.
- Brittle material: Brittle materials like chalk are weak in tension. If the plane where applied tension exceeds the strength of the chalk, the chalk will break.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author



why do cracks act at 45 degree is incomplete
Updated. I appreciate your interest in reading the article.