Let us start with the basic definition of modular ratio. It is the ratio of elasticity modulus of two different materials. For example, let the value of elasticity modulus of two different material is E1 and E2. Then the value of modular ratio “m” is :
$$m = \frac{E1}{E2}$$
In the case of reinforced concrete structure modular ratio is the ratio of elasticity modulus of steel and concrete. The value of stresses in concrete and steel is related using modular ratio. As the strain in the reinforcing steel and concrete is linear in nature.
It is very much important to consider the value of modular ratio when we want to analyze the composite sections like reinforced concrete structures.
The fundamental assumptions in flexural theory is that plane cross section remains plane, even after bending. This is only valid when we can ensure the proper bonding between both the materials (reinforcement and concrete) to act as an integral unit.
For analysis we express the stress of material1 in terms of the corresponding stress of material 2.
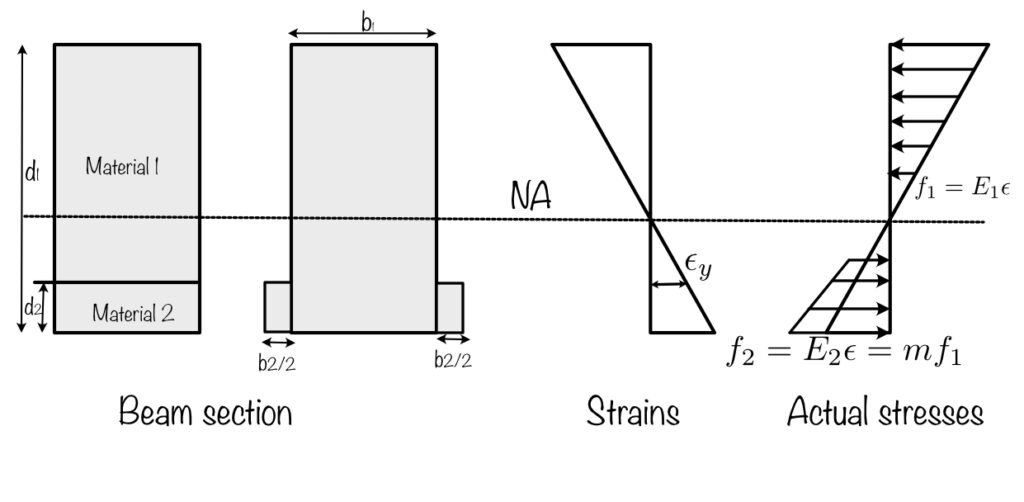
Engineers use this information to optimize the design of beams and ensure that they are able to bear the loads and stresses. We also use the modular ratio to compare the stiffness of different materials and how they interact with one another.
Conclusions
In conclusion, the modular ratio is a crucial concept in the analysis and design of beams. Additionally, understanding the modular ratio can help engineers to optimize the design of beams and improve the overall safety and performance of structures.
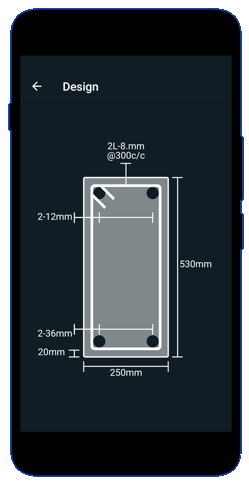
Beam design
- RCC Beam Design is a free app for designing reinforced concrete beams as per Indian Standards.
- RCC Design and detailing could be performed by Limit State Method specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


