Let us consider an example where a beam is initially in unstressed position. Now when a uniform bending moment is applied along the length of beam , then the beam will bend. When the beam bends the top surface of the beam is in tension and the bottom surface is in compression. So it is quite evident that at some mid surface the value of stress will be zero i.e., neutral axis.
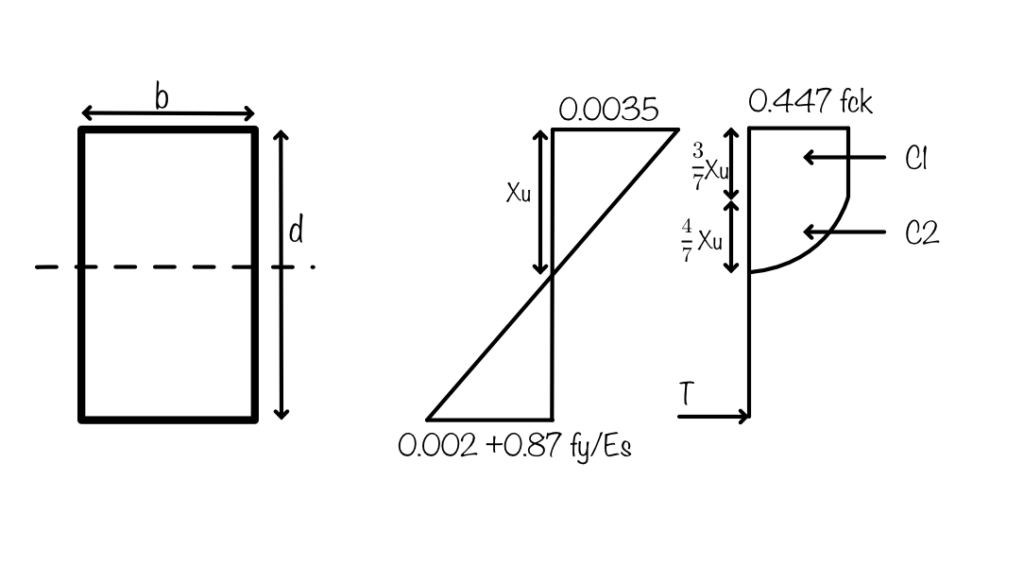
Neutral axis is basically an axis where the value of stress is zero, or the axis of transition from compression zone to tension zone. The location of neutral axis can be determined by applying the static equilibrium conditions. In a rectangular beam section the value is computed easily by the following equation of calculating moment of resistance.
$$ M_{uR} = C_u . z = T_u . z $$
where Cu and Tu are the compressive and tensile forces respectively.
$$ T_u = f_{st} A_{st} = 0.87 f_y A_{st}$$
$$ C_u = 0.447 f_{ck} b [\frac{3 x_u}{7} + (\frac{2}{3} \times \frac{4 x_u}{7})] = 0.362 f_{ck} b x_{u}$$
The depth of neutral axis should be such that :
$$C_u = T_u $$
$$x_u = \frac{0.87 f_y A_{st}}{0.362 f_{ck}b}$$
You can calculate the maximum value of Xu is using the following formula:
$$x_{umax} = \frac{0.0035}{0.0055 + 0.87 f_y/ E_s} * d $$
The value of maximum value of neutral axis depends on the grade of steel.
| Grade of steel | xu /d |
| Fe 250 | 0.5313 |
| Fe 415 | 0.4791 |
| Fe 500 | 0.4560 |
Check this post to know the detail procedure of design of RCC beam
Beam design
- RCC Beam Design is a free app for designing reinforced concrete beams as per Indian Standards.
- RCC Design and detailing could be performed by Limit State Method specified in IS456:2000
- Option to save the design projects in local storage.
- Detailed calculation steps presented for verification and validation.