In the engineering first year all of us have to go through the mechanics course. This course deals with the force and reaction in the body, inertia, moment, vector, scalar and so on. After that we have strength of material or Mechanics of solid course, and Fluid Mechanics course. In higher semester we go through soil mechanics course. All these courses follow same principal but differs in the constitution of body. How we are assuming the basic material that will govern the underlying phenomenon. Like in engineering mechanics course basic assumption with the body is that, it is a rigid body. Hence, we only bother about the external reaction and displacement of the body. In the mechanics of solid course the body is deformable body. That means on applying force it deforms. Due to this deformation some internal forces generate. But the deformable body resists the change, which is not there in case of fluid mechanics. In the mechanics of solid and fluid mechanics the body is continuum. Later on we will see the details about the continuum. Soil mechanics is the mechanics of particle. This particle mechanics will govern the behavior of soil.
Today we are going to learn some basic concepts which we generally ignore as it appear very obvious to us. But it has very deep meaning inside, and helps understand the mechanics of solid better.
Some basic terminologies in solid mechanics:
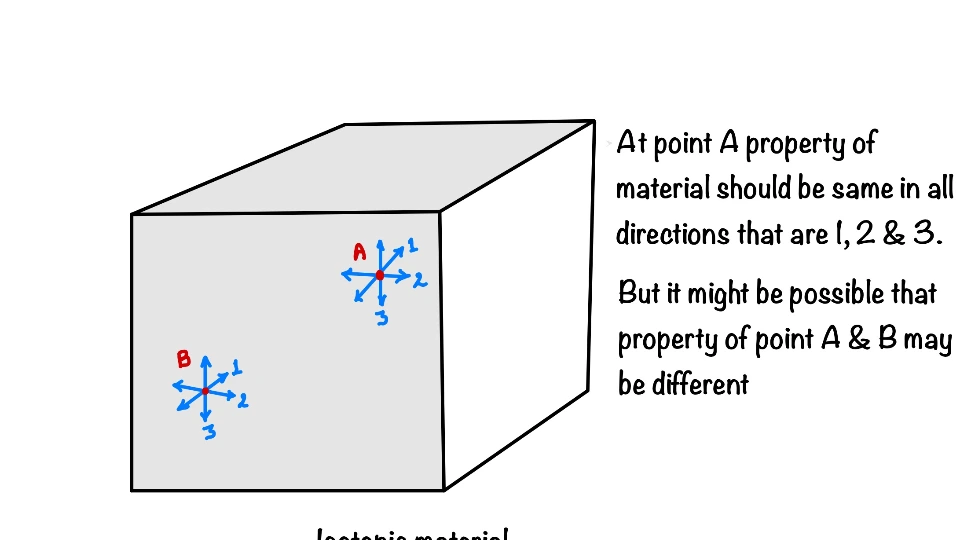
Isotropic material:
Many times we will come across this word isotropic. So if any material is isotropic in nature that means, it has the same material property in each direction of the body.
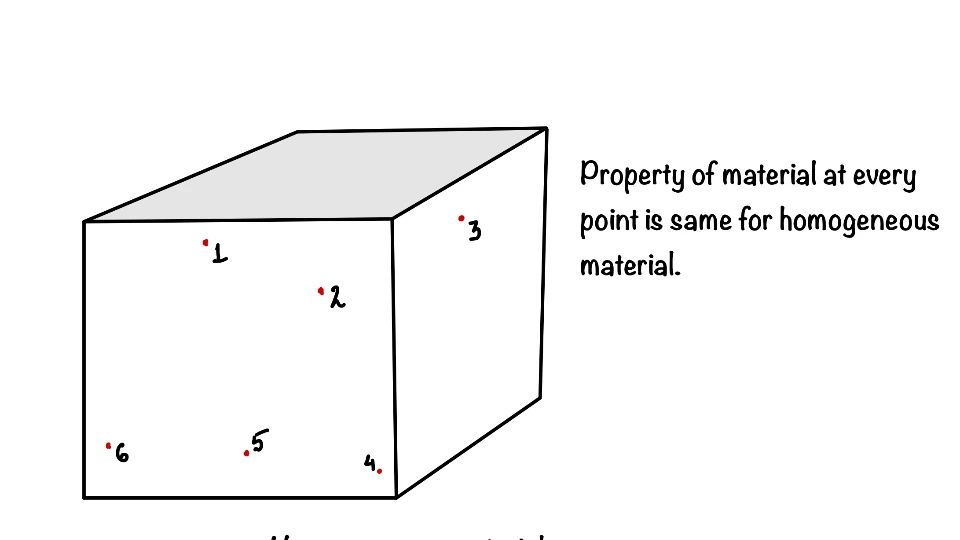
Homogeneous material:
If material is having same property at every point inside the structure it is called homogeneous material. Homogeneity give the space symmetry where as isotropic means directional symmetry.
Continuum body in solid mechanics:
Any material is made up of molecule, the concepts of continuum assumes the continuous distribution of mass within the matter or system with no empty space. Continuum is the kind of idealization for continuous description of mass. How it is useful for us? So, you can think it in this way that if you take sample from anywhere of the body, every time you will get same sample. Every sample is the perfect representation of the body.
Deformable body:
As we know that, in theoretical mechanics we deal with the rigid bodies but in the strength of material the body is deformable. That means, the body has the ability to change its initial shape and dimension under the action of external loads.
Than you can think that if body was in equilibrium, then after deformation loads might change its position due to deformation, how to analyze the structure. So, answer to this is, the deformation is very small as compared to the dimension of the body. Hence, we can easily ignore the deformation.
Elasticity:
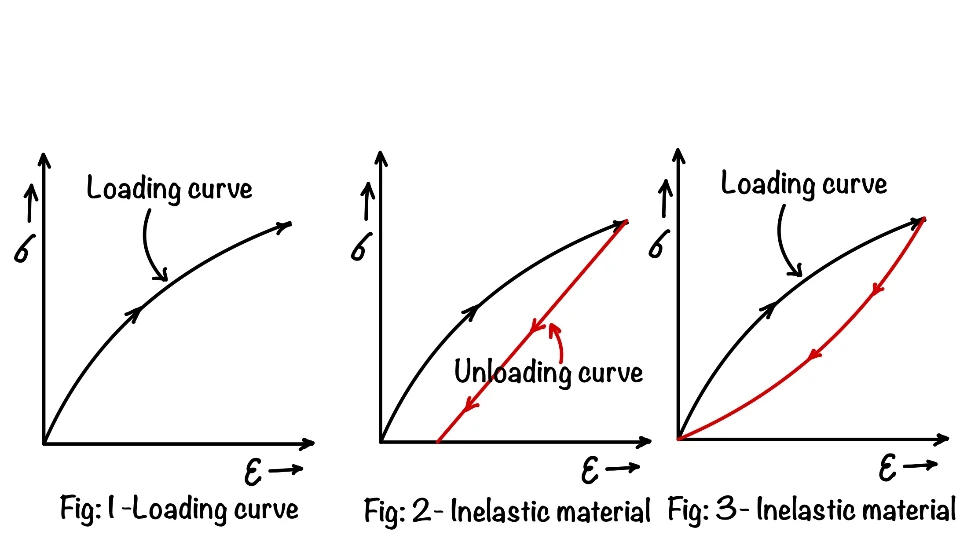
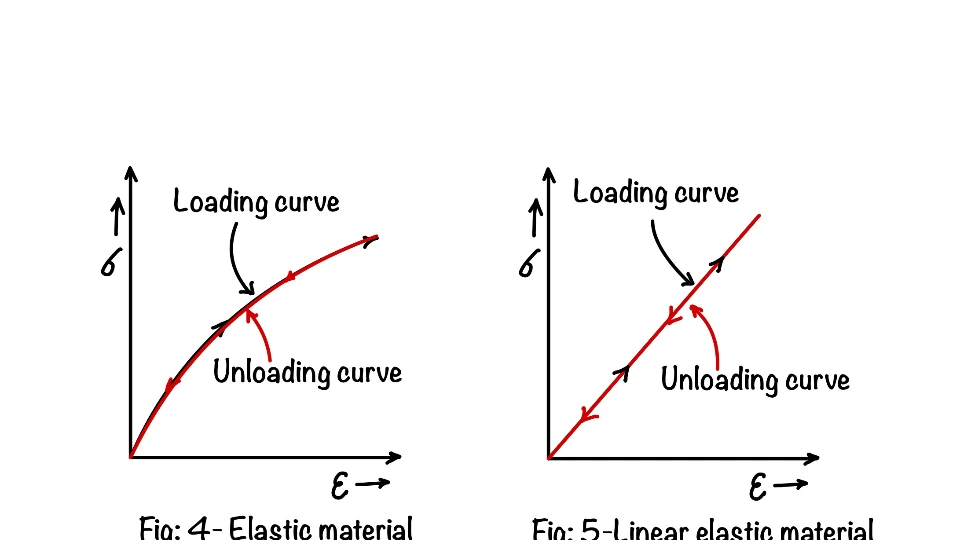
We have defined in our junior classes as, when we remove the applied load from the material, and if material regains its shape then we call it a elastic material. This definition holds good, only few improvement over it we need to learn. It’s not only the final position of the material which matter, the path of recovery also matters as shown in the Fig below. First figure shows the loading curve of any material, in second curve we can see the recovery is not full then it is inelastic. In the third figure the recovery is full but the path of recovery is different, hence this is also not elastic material. In fourth figure the path and final recovery both are same hence this the perfect elastic material. The material in the fifth figure is linear elastic material.
- Strength: Strength is the stress bear by the structure just before failure point.
- Stiffness: It is the ability of the structure to resist the strain caused by the external force acting on it.
Also read: What is stress?
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


