Carnot efficiency is an often-heard term for heat engines, including those used in bikes, scooters, or airplanes. Acting as a benchmark and defining how efficient any engine can be, are some of its main practical implementations. But what it is and how it can be calculated is described in this post.
Carnot Efficiency – The Efficiency of Carnot Engine
Carnot efficiency describes the maximum possible thermal efficiency that any heat engine can attain without breaking the laws of nature. It acts as a benchmark for any heat engine.
The credit behind setting this benchmark goes to the French engineer Sardi Carnot, who proposed a thermodynamic cycle that can achieve maximum possible thermal efficiency working between two temperature limits.
The Carnot efficiency answered a critical question how efficient could any engine be? Is the answer 100%? No. Sardi Carnot answered this, the complete conversion of a heat engine into work is impossible. And as a result, the efficiency achieved by the Carnot engine gives the maximum theoretical achievable thermal efficiency.
It is defined as the ratio of the net work done by the Carnot cycle to the heat absorbed by it. From the First law of Thermodynamics, we know that for a cyclic process, the net work done is equal to the net heat transfer by the system. This gives the mathematical efficiency of any thermodynamic cycle, including the Carnot cycle.
$$\eta_{thermal} = \frac{ W_{net} }{ Q_{in} } = \frac{ Q_{in} – Q_{out} }{ Q_{in} }$$
Carnot Engine
The Carnot engine is a theoretical engine that works on the Carnot cycle operating between two temperatures, T1 (source) and T2 (sink). These temperatures limit the working temperature between which these engines operate. The Carnot cycle, the thermodynamic cycle defined for this engine, estimates the maximum possible efficiency a heat engine can achieve working between those temperatures.
Even though any engine can have irreversibilities in the form of friction and non-quasi-static behavior. The French engineer Nicolas Leonard Sardi Carnot proposed a cycle that can eliminate these irreversibilities and set a benchmark for the heat engine.
Carnot engine efficiency formula
The formulation of the Carnot efficiency is the simplest formula you can come across in thermodynamics. It is simply a ratio of temperature deference and source temperature.
Mathematically, the Carnot efficiency is:
$$\eta_{Carnot} = \frac{ T_h – T_l}{T_h} = 1 – \frac{T_l}{T_h}$$
where Th and Tl are the temperatures of the heat source and heat sink, as shown in the figure below.
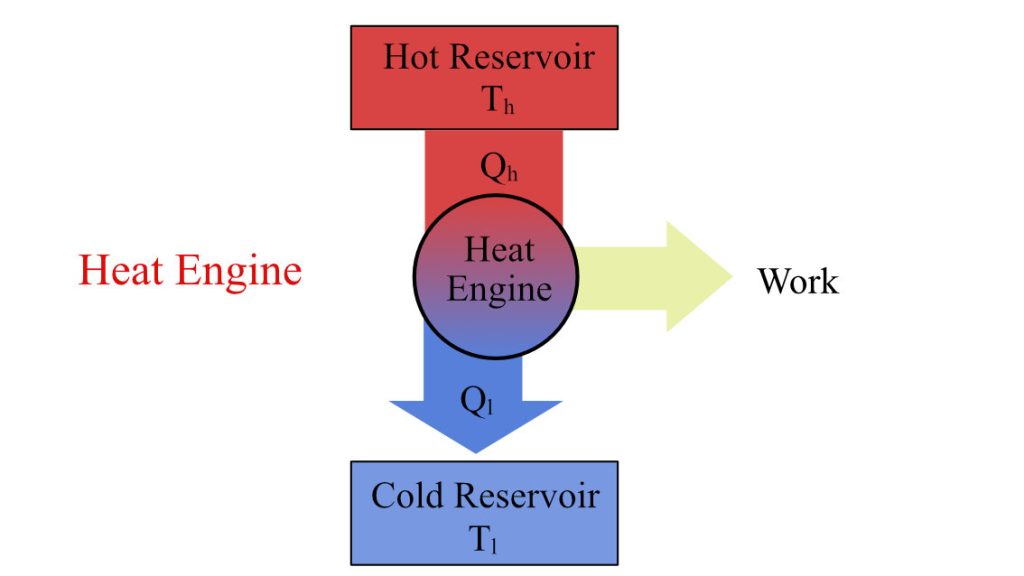
Derivation of the Carnot engine efficiency
The Second Law of Thermodynamics describes heat as low-grade energy and work as high-grade energy. And the complete conversion of low-grade energy into high-grade energy is not possible. This limits the complete conversion of supplied heat into work.
For the above Carnot engine, the thermodynamic cycle, i.e., the Carnot cycle, looks like this:
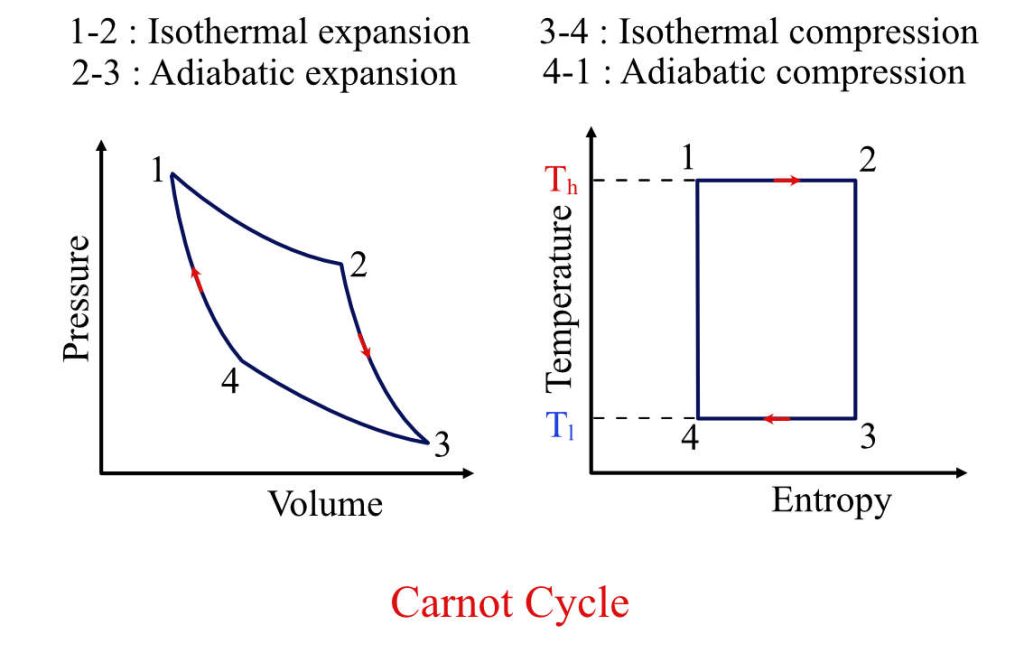
It comprises four processes two isothermal processes and two isentropic processes:
- Isothermal process: Processes 1-2 and 3-4 are isothermal processes, i.e., the temperature remains constant.
- Isentropic process: Processes 2-3 and 4-1 are isentropic processes, i.e., there is no heat transfer across boundaries.
For this cycle, the thermal efficiency is:
$$\eta_{thermal} = \frac{ Q_{in} – Q_{out} }{ Q_{in} } = 1 – \frac{Q_{in}}{Q_{out}}$$
For isothermal processes 1-2 and 3-4, the heat transfer is equal to the work done during that process. This makes Qin and Qout equal to the work done during those processes.
$$\eta_{Carnot} = 1 – \frac{ T_l \ln(V_3/V_4)}{T_h \ln(V_2/V_1)}$$
where Tl and Th are the temperatures of reservoirs. And V1, V2, V3, and V4 are the system’s volume at those states. By applying the isentropic process property, we get that the ratio of volumes is equal. Thus, efficiency becomes
$$\eta_{Carnot} = 1 – \frac{Tl}{Th}$$
Conclusions
It is visible that no engine can be perfectly efficient in converting heat energy to work. The same goes for the Carnot engine. But these engines don’t have friction and act as benchmarks. The efficiency of the Carnot engine defines the maximum efficiency and corresponding work you can obtain from any system.
Some key learnings from the post:
- Carnot efficiency: Carnot efficiency describes the maximum possible thermal efficiency that any heat engine can attain without breaking the laws of nature.
- Carnot efficiency formula: It is defined as one minus the ratio of temperatures of the cold reservoir and hot reservoir.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.