Design of tensile members

We have seen design examples to determine the tensile design strength for structural steel sections. Let us explore on how to design a tensile member and learn the simple design steps.

What are the basic information needed to start the design?

To design a tensile member, the following things are required:

Length of the member
End plate connections
Load it has to support $($ also called design tension load, $T)$

Now a tension member should be designed such that it’s design tensile strength, $T_d$ should be greater than design factored load, $T$ i.e., $T_d>T$ .

Design: an AB process → Assumption and Backing

It is obvious that the designer has to select a cross-section such that $T_d>T$ (for the member to resist load)

For tensile members, the design tensile strength $T_d$ is minimum of $T_{dg}, T_{dn}, T_{db}$ .

Item	Formula	Main Ingredient	Design Step
$T_{dg}$	$A_gf_y/\gamma_{m0}$	Cross-section Area	Assumption of cross-section
$T_{dn}$	$0.9A_nf_u/\gamma_{m1}$	Net-section Area	Design of end connection (Number of bolts, Weld length)
$T_{db}$	$T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}}$ $T_{db_2}=\frac{0.9A_{vn}f_u}{\sqrt{3}\gamma_{m1}}+\frac{A_{tg}f_y}{\gamma_{m0}}$	Shear plane and Tension plane area calculation	Design of end connection (Number of bolts, Weld length)

The table above shows the main assumption and design overview.

Thus, a designer has to adopt following two steps:

Step A: Assumption → Assume a cross-section. Design the end connection for it.
Step B: Backing → Use design equations of IS 800:2007 to compute $T_d$ such that $T_d>T$

Let us look at the design steps with a design example.

Step-by-step procedure of design of tension member

Design Example: Design a 2.5 m long single section angle acting as a tension member in a bridge truss. The member is subjected to a factored load of 280 kN. Assume the gusset plate thickness as 16 mm and the diameter of bolts to be used as 20 mm of grade 8.8. Assume Fe 410 grade of steel.

Step 1: Calculate the required area of cross-section taking $T_{dg} = T$

Here,

$T=280\; kN$ and $T_{dg}=A_gf_y/\gamma_{m0}$

Hence, Area required $A_g=T_{dg}\gamma_{m0}/f_y$

$= 280\times 10^3\times 1.\frac{1}{250}=1232\; mm^2$

Step 2: Adopt a trial section from SP 6:Part 1 for the required gross-area $A_g$

Let us try ISA $90 \times 60 \times 10$ mm. Hence we have,

Gross area, $A_g=1401\; mm^2$

Design of end connection (Number of bolts required, Length of weld)

The design equations to determine the strength of bolt, $V_{ ds}$ is given in article.

$V_{ ds} =Min (V_{dsb}, V_{dpb})$

$V_{ dsb}$ for M20 8.8 grade bolt

V_{dsb}=\frac{f_{ub}}{\sqrt{3}\gamma_{mb}}(n_nA_n+n_sA_s)

Here, for grade 8.8 bolt, $f_{ub} =800 \; MPa$

$n_n=1;\; A_n=0.78\times \frac{\pi}{4}\times (20)^2=245\; mm^2$

Hence, $V_{dsb}=(800\times 245)/(\sqrt{3}\times 1.25)=90.53\;kN$

$V_{ dpb}$ for design problem

V_{dpb}=2.5 k_bdt\frac{f_{u}}{\gamma_{mb}}

where,

k_b=Min (e/3d_0,p/3d_0-0.25, \frac{f_{ub}}{f_u}, 1.0)

IS code recommendation

In a design problem of tension members, $p,e$ will not be provided. In such a case, use IS 800: 2007 provisions to meet minimum requirements and select $p,e$ .

Item	Minimum as per IS 800:2007	For current problem
$e$	$1.7 \times d_h$ or $1.5 \times d_h$ depending on hand-flame cut or machine-flame cut respectively.	$1.7 \times d_h=1.7\times22=37.4 \; mm$ Provide $e=40\; mm$
$p$	$2.5 \times d$	$2.5\times d = 2.5 \times 20 = 50\; mm$ Provide $p=60 \; mm$

Application of recommendation

Therefore,

k_b=Min (e/3d_0,p/3d_0-0.25, \frac{f_{ub}}{f_u}, 1.0)

k_b=Min (\frac{40}{3\times 22},\frac{60}{3\times22}-0.25, \frac{800}{410}, 1.0)

Hence,

k_b= 0.606

Thus,

V_{dpb}=2.5 k_bdt\frac{f_{u}}{\gamma_{mb}}

V_{dpb}=2.5 \times 0.606\times 10\times 20\times\frac{410}{1.25}=99.38\; kN

Hence, $V_{ds} =Min (V_{ dsb }, V_{ dpb}) =90.53 \; kN$

Thus, number of bolts required, $n =\frac{280}{90}.53 =3.1 \simeq 4$

Thus, provide $4$ M20 bolts of grade $8.8$ at a pitch of $60 \; mm$ and edge distance $40\; mm$ .

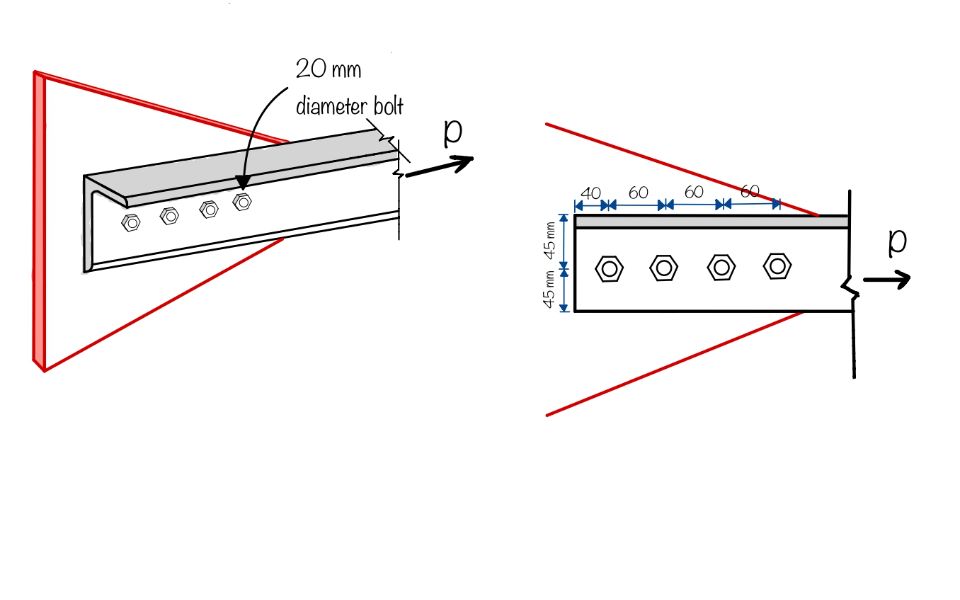
Step 4: Determine $T_{dn}, T_{db}$ to check if $T_d>T$

For $T_{ dn}$

As per the end plate design, we arrived at a requirement of $4$ bolts of grade $8.8$ at a pitch of $60 \; mm$ and edge distance $40\; mm$ .

Therefore, $A_{nc}=(90-20-5)\times10=650\; mm^2$ [Refer to article]

Now, $A_{go}=(60-5)\times10=550\; mm^2$

As per clause 6.3.3 IS 800 :2007,

T_{dn}=0.9A_{nc}f_u/\gamma_{m1}+\beta A_{go}f_y/\gamma_{m0}

where,

$\beta=$ $1.4-0.076(w/t)(\frac{f_y}{f_u})(\frac{b_s}{L_c})\leq(f_u\gamma_{m0}/f_y\gamma_{m1})\geq 0.7$

For the current scenario,

$w=$ outstand leg width $=60 \,\text{mm}$ ;

$b_s=$ shear lag width $=60+45-10=95 \,\text{mm}$ ;

$L_c=$ Length of end connection $=3\times60=180 \,\text{mm}$ ;

$A_{nc} =$ Net area of the connected leg $=650 \,\text{mm}^2$ ;

$A_{go} =$ Gross area of the outstanding leg $=550\; mm^2$ ;

$t=$ Thickness of the leg $=10\; mm$

Hence, $\beta=1.253$

Therefore, $T_{dn} =349.13 \;kN$ $>300\; kN$ . Hence OK.

For $T_{ db}$

Refer to figure below

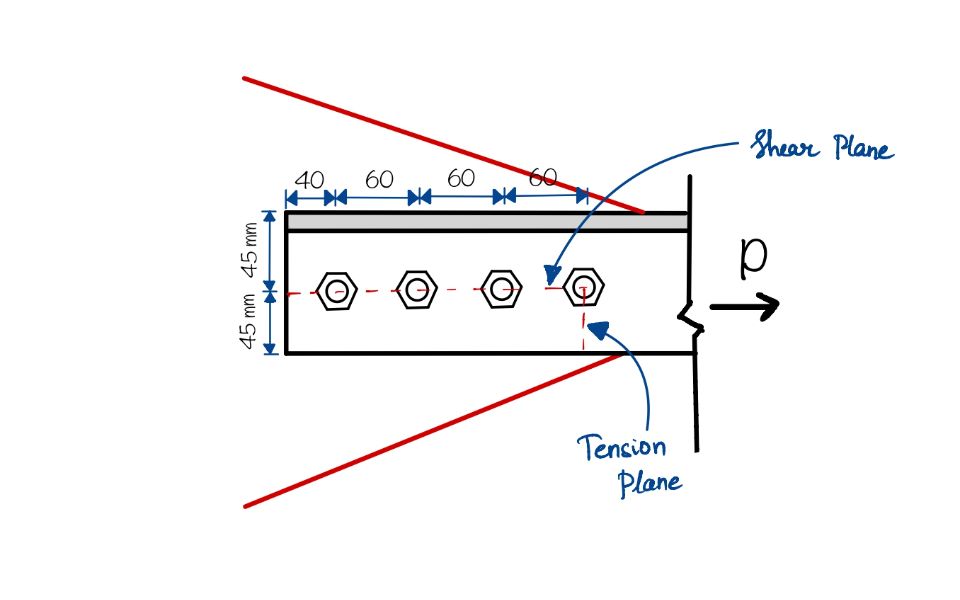
$A_{vg} =220 \times 10= 2220 \,\text{mm}^2$

$A_{vn} = [220 - (3.5 \times 22)] \times 10 = 1430 \, \text{mm}^2$

$A_{tg} = 45\times 10 = 450 \; mm^2$

$A_{tn} =(45 - 0.5\times 22) \times 10 = 340\; mm^2$

Hence,

T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}}

T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}}

T_{db_1}=\frac{2220\times250}{\sqrt{3}\times1.10}+\frac{0.9\times340\times410}{1.25}= 391.67\; kN

T_{db_2}=\frac{0.9A_{vn}f_u}{\sqrt{3}\gamma_{m1}}+\frac{A_{tg}f_y}{\gamma_{m0}}

T_{db_2}=\frac{0.9\times1430\times410}{\sqrt{3}\times1.25}+\frac{450\times250}{1.10}=346\; kN

Hence, $T_{db}=346\; kN > 280 \; kN$

Conclusions

In this section we have learned the following key points:

Failure modes: We have learned the different failure modes for the members subjected to tension. Like failure by net area rupture, gross section yielding, and block shear failure.
Net area: In this article, we have learned how to calculate the net area of the cross-section.