What is Development Length for Reinforced Concrete Footings as per IS456

To understand development length, you must visit the article “What is development length.” If you have already gone through the article, you must know that development length is the grip available to hold the rod in position. In this article, we will see the application of development length while designing the footing.

The formula for development length as per IS-456:2000

Now you can feel the requirement of the development length. After this, we can discuss the codal requirement for development length. IS-456:2000, in clause 26.2.1, says that the bar must develop the required tension or compression, which we can assure by development length check. You can calculate it by:

$$ L_{\mathrm{d}}=\frac{d_b f_{\mathrm{s}}}{4 \tau_{\mathrm{bd}}} $$

where:

• $d_b$ is the nominal diameter of the bar,
• $f_s$ is the stress in the bar at the section considered at design load (for fully stressed bar, $f_s = 0.87 f_y$)
• $\tau_{bd}$ is the design bond stress as per the table below.

\begin{array}{|l|l|l|l|l|l|} \hline {\text { Grade of concrete }} & \text { M20 } & \text { M25 } & \text { M30 } & \text { M35 } & \text { M40 and above } \\ \hline \text { Design bond , MPa } & 1.2 & 1.4 & 1.5 & 1.6 & 1.9 \\ \hline \text { For fully deformed bars } & 1.18 & 1.37 & 1.54 & 1.71 & 1.87 \\ \hline \end{array}

• For a deformed bar in tension, τbd values can be increased by $60\%$
• For bars in compression, the value of the bond in tension can be increased by $25\%$.
• In case of nominal reinforcement is provided, $\tau_{bd}$ is taken as 1.0 MPa.

$$ L_{\mathrm{d}}=\frac{0.136d_b f_{\mathrm{s}}}{ \tau_{\mathrm{bd}}} $$

Development length checks in footing.

In this post, we are discussing isolated footings. Generally, we design footing as a wide beam. And we divide footing behavior as one-way shear and two-way shear. Please see the post on the design of the footing for more detail. However, for completeness, we are again producing an image here. So that users can understand the critical points.

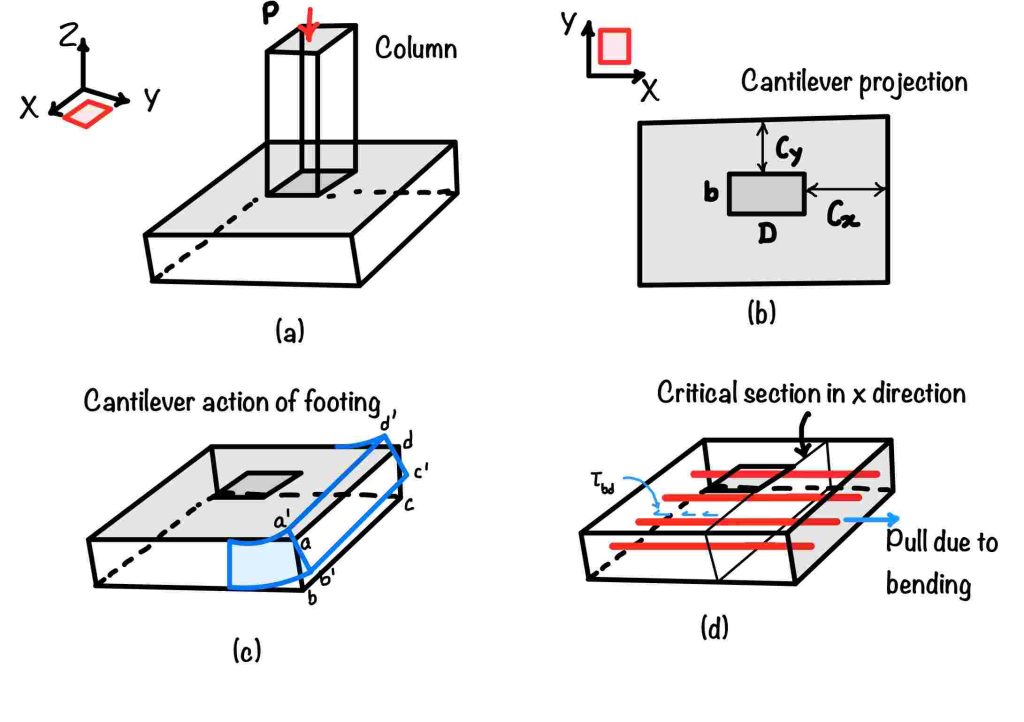
Now, if you want to check the for bending about $x$-axis as you can refer in the part (d) and (b) of the figure.

$$L_{d,\text{reqd}} = L_{dx} = \frac{0.87 f_y}{4\tau_{bd}} \times \phi_x, L_{d,\text{available}} = C_x$$

For bending about $y$-axis:

$$L_{d,\text{reqd}} = L_{dx} = \frac{0.87 f_y}{4\tau_{bd}} \times \phi_x, L_{d,\text{available}} = C_y$$

Where $\phi_x$ and $\phi_y$ are the diameters of the bar for bending about $x$- axis and $y$ – axis, respectively.

? If  available development length is more than the required development length the check for development length is correct.

The critical case

If the check for development length is already discussed, what do we have to check for? Generally, this check only works when the soil has a large bearing capacity. In that case, the size of the footing required becomes very small, which leads to lesser cantilever projections. You can take the following remedies in this case:

1. Reduce the area: You can reduce the area of the bar. By doing this, we can reduce the required development length.
2. Increase the footing: You can increase the size of the footing such that the projection $C_x, C_y$ is not less than the required development length.
3. Provide bend: Bends increase the available development length. This method also can help you in a critical situation.
4. Increase steel area: Increasing the area of steel will also modify the development length requirement. You can calculate it as:

$$ L_{dm}=\frac{A_{s,\text{reqd}}}{A_{s,\text{provided}}}\times L_d $$

Conclusions

You can check the required development length in footing by simply using the formula. The only thing you have to keep in mind is that you have to check for bending in $x$ and bending in $y$. The special case arises when we build the foundation in the soil with large bearing pressure. As the size of the footing reduces.

In this post, you have learned the following key points:

• Development length: You have to check the footing for both directions.
• Critical case: When the footing is placed in soil having a large bearing capacity, the footing size decreases. This reduction in the size of the footing creates a problem in providing the space for the required length.
• Remedies: You can increase the area of steel, reduce the diameter of the bar, increase the footing, or you may provide the $90^\circ$ bend to make it safe for development length.