When you hold the scale from one end and just support it from the other end with finger (you can refer the figure). The scale behavior will change as the end conditions are different. In this article we will derive the differential equation for this column apply the boundary condition and calculate the critical load for fixed-pin column.
What are the assumptions in Euler’s critical load?
The Euler’s critical load is derived for the pinned condition, as we have derived in the previous article. We are again writing the assumption while deriving the critical load for other end conditions.
Euler’s critical load has the following assumptions:
- The axis of the column is perfectly straight when unloaded.
- The line of thrust co-insides with the unrestrained axis of the column.
- Flexural rigidity $EI$ is uniform.
- Material is isotropic and homogeneous.
What is differential equation for column with fixed-pin end
When you see the part (a) in the figure. The load P is acting in the column and the column is having pin end and fixed end conditions.
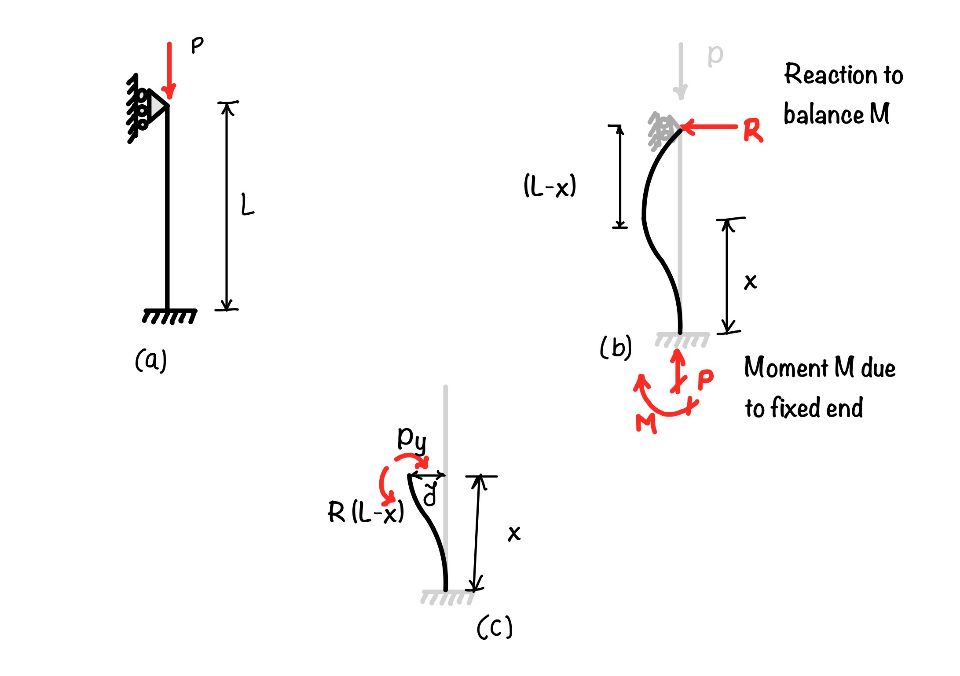
$$ EI\frac{d^2y}{dx^2}=R(L-x)-Py \\ EI\frac{d^2y}{dx^2}+Py= R(L-x) $$
$$ y=C_1\sin{\sqrt{\frac{P}{EI}}}x+C_2\cos{\sqrt{\frac{P}{EI}}}x +\frac{R(L-x)}{P} $$
What are boundary condition for fixed-pin end conditions
You can see the figure to apply the end condition for fixed-pin column. For this case, the end conditions will be as follows
$$ \text{ at }x=0 , y=0\\ \text{ at } x=0 , \frac{dy}{dx}= 0 \\ \text{ at } x=L, y=0 $$
Now consider the equation for the fixed, hinged condition. Just recall the equation
$$ y=C_1\sin{\sqrt{\frac{P}{EI}}}x+C_2\cos{\sqrt{\frac{P}{EI}}}x +\frac{R(L-x)}{P} $$
Now when we put $x=0$ in the above equation the first term $C_1\sin{\sqrt{\frac{P}{EI}}}x$ will be zero and the second term $C_2\cos{\sqrt{\frac{P}{EI}}}x$ will become $C_2$. Because the $\sin \theta =0 \text{ and } \cos \theta \text { at } \theta = 0$ . Hence we can compute the value of $C_2$ as :
$$ \text{ at }x=0 , y=0 \Rightarrow C_2 = -\frac{RL}{P} $$
Now to apply the second boundary condition in the equation, we need to compute the derivative of the equation.
$$ \frac{dy}{dx}=C_1\sqrt{\frac{P}{EI}}\cos{\sqrt{\frac{P}{EI}}}x-C_2\sqrt{\frac{P}{EI}}\sin{\sqrt{\frac{P}{EI}}}x -\frac{R}{P} $$
Now putting the boundary values in this equation we will get
$$ \text{ at } x=0 , \frac{dy}{dx}= 0 \Rightarrow C_1 = \sqrt{\frac{EI}{P}}\times \frac{R}{P} $$
Now after knowing the values of $C_1$ and $C_2$, we can replace the values in the above equation.
$$ y=\sqrt{\frac{EI}{P}}\sin{\sqrt{\frac{P}{EI}}}x-\frac{RL}{P}\cos{\sqrt{\frac{P}{EI}}}x +\frac{R(L-x)}{P} $$
Now putting the third end condition that at $x=L$, $y=0$
$$ \tan \sqrt{\frac{P}{EI}}L =\sqrt{\frac{P}{EI}} $$
The smallest root of this equation gives
$$ \sqrt{\frac{P}{EI}} = 4.4934 \text{ rad }\\ P_{cr}=\frac{2\pi^2EI}{L^2} $$
Conclusion
Euler’s formula was derived for the pin condition column. But in reality we found different type of columns with different end condition. Hence, in this series of post we are trying to find the critical loads for columns having different end conditions. And, in this article we have discussed the column with fthis end condition. In the next post we will do this for the fixed-free end condition.
You have learned the following key points in this post:
- Critical Load: When a column is supported with one end fixed, and other end pin, the critical load for the column will be $ P_{cr}=\frac{2\pi^2EI}{L^2}$.
- Equivalent length: When compared with the Euler’s load, you can compute the equivalent length for this column. Which is equal to $L/\sqrt{2}$.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


