Whenever there is a discussion about the thermodynamic processes, there is a discussion about the quasi-static process. These are the process that requires infinite time to complete. But are these processes practically possible?
In this blog post, you will get an answer to that and learn about the quasistatic process.
Quasi-static process
The quasi-static process, also known as the quasi-equilibrium process, refers to an idealized process that happens extremely slowly so that the system remains in internal thermodynamic equilibrium. The term quasi-static means ‘almost static’. Therefore, these processes are considered almost static, i.e., the rate of change of system properties is practically negligible.
The need for a system to be in thermodynamic equilibrium throughout the process is crucial to define the macroscopic state of the system at each instant of the process. The process can be shown with a well-defined path in graphical representations.
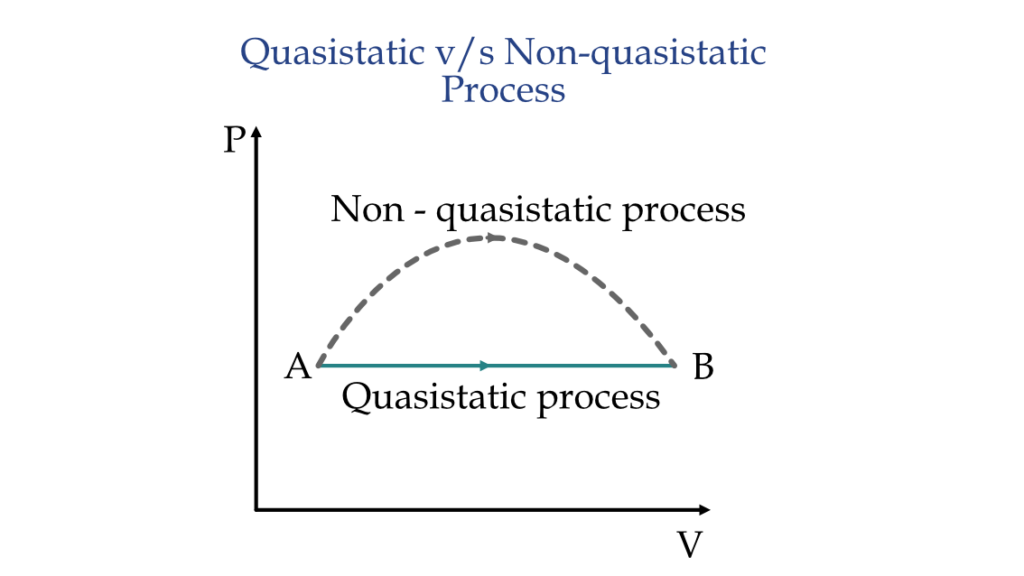
For any process to be quasi-static, it needs to have:
- Infinitesimally slow rate: the rate of change of the system properties needs to be infinitesimally low.
- Intermediate states in equilibrium: the intermediate states during this process has to be in thermodynamic equilibrium with the surrounding all the time.
The quasi-static process can not be physically seen in nature because there is no finite change in the system properties. And as a result, no process in nature is quasi-static, and the completion time of such a process is infinite.
Even though no process in nature is quas-static; but, practical applications require well-defined intermediate system properties to quantify the change in properties. As a result, all the processes are analyzed, considering them quasi-static.
For example, the melting of ice at a constant temperature. A piece of ice kept in a container at 0° C when heated by the addition of a small heat with time will result in the melting of the ice. And by keeping the heating addition extremely small, the process becomes quasistatic.
Reversible process
Reversible processes are quasi-static processes with no dissipation effect. As a result, all reversible processes are quasi-static in nature.
This also means that a quasi-static process can be a non-reversible process when there are dissipation effects in the form of friction or other losses.
For example, reversible adiabatic process, reversible isothermal process, etc.
Work done in the Quasi-static process
For these processes, the intermediate stages remain in thermodynamic equilibrium with the surrounding. As a result, these processes have well-defined paths.
The work done for the such process are:
- Isothermal process: For these processes, the change in temperature remains zero, i.e., throughout the process, the system’s temperature remains constant. For these processes, the work done becomes:
$$ W = mRT \ln (\frac{T_f}{T_i})$$
- Isobaric process: These are the process for which the change is pressure remains zero, i.e., throughout the process, the pressure within the system remains constant. The work done for such a process is:
$$ W = P(V_f – V_i)$$
- Isochoric process: For these processes, the change in volume remains zero, i.e., throughout the process, the system’s volume remains constant. Since there is no volume change; therefore the work done for such a process is zero:
$$ W = 0$$
Conclusions
The quasi-static process is a thermodynamic process, characterized by an infinitesimally small change in system properties. And as a result, the completion time of such a process is infinite. Even though no process in nature is quasi-static; but, for practical applications, all the processes are analyzed, considering them quasi-static.
Some key learnings from the post:
- Quasi-static process: An idealized process that happens extremely slow such that the system remains in internal thermodynamic equilibrium throughout the process.
- Reversible process: The quasi-static process with no dissipation effect.

Android Apps
⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)
At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.
Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.