To understand the stress, let’s do one demonstration. Pick the eraser on your table and try to compress it. When you release the pressure, the eraser returns to its original shape. So who is bringing the eraser to its original form? As per Newton’s second law, there has to be a force.
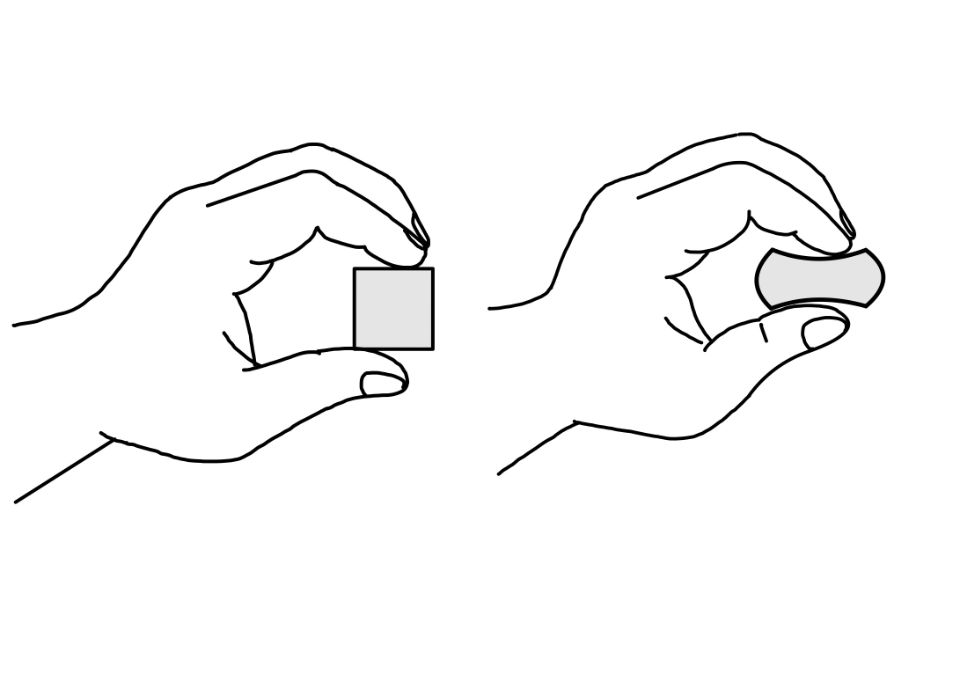
The mysterious force is being generated by the stress. It is the internal resistance of the body which creates stress, and this stress creates the equivalent force. You will learn the stress, its cause, and its effect in this article. You will also learn how stress is different from pressure.
What is stress?
As we have discussed in the introduction of the article, stress is internal resistance. The material offers this internal resistance to the distorting effects of an external force. We will define stress as the force across a small boundary per unit area of that boundary.
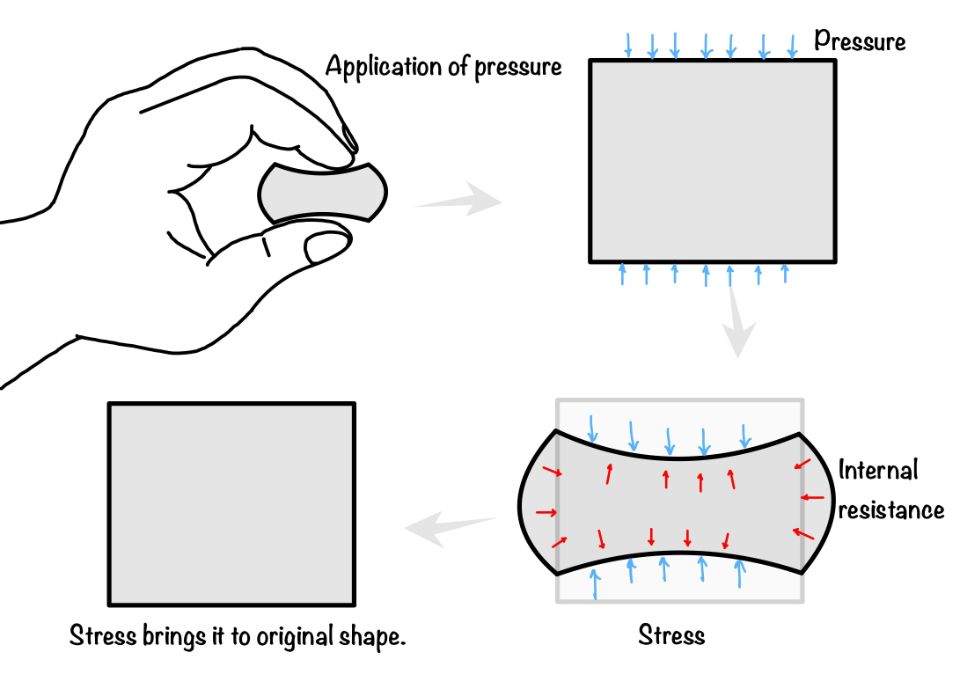
We know one another term which we define as the force per unit area. So yes, you are right its pressure. So the pressure is the applied force per unit area, whereas stress is the internal force (generated to resist the deformation) per unit area.
In other words, you can apply the pressure, but you can not apply the stress. Stress is a completely hypothetical quantity. That is why you don’t know any instrument which is used to measure stress.
As we have discussed, stress is a hypothetical quantity. Nevertheless, we use it for our better understanding. Hence to simplify it further, we separate the stress into two parts. Therefore we divide the stress into normal and shear stress on the basis of the force that caused deformation.
Normal stress
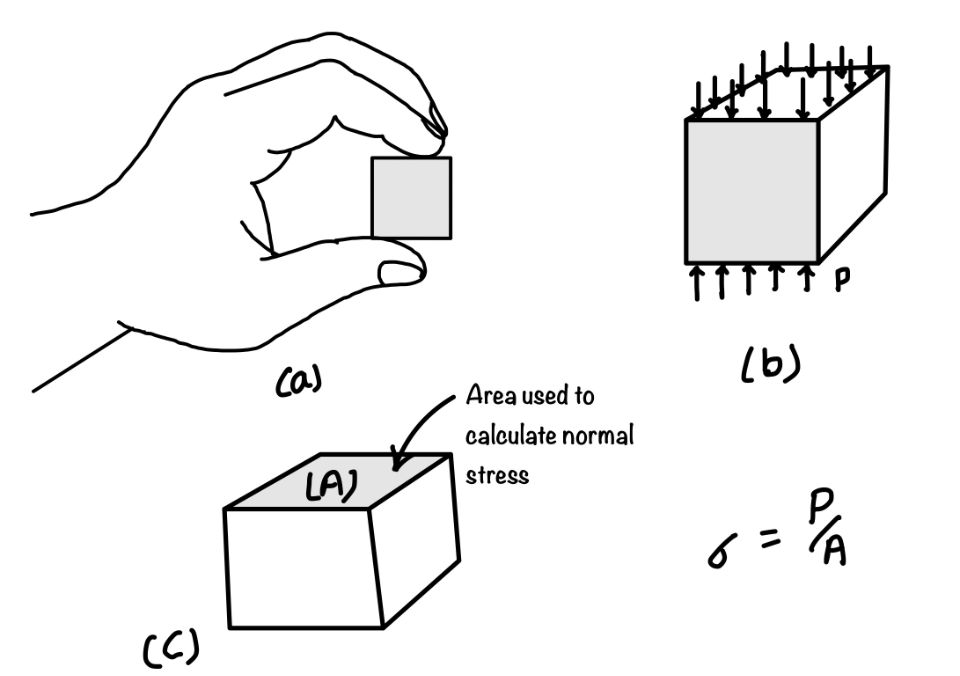
As it is clear from the name, it is the stress perpendicular to the eraser’s cross-sectional area. We may develop the normal stress by stretching the material cross-section in the normal direction. Normal stress is represented by the Greek letter $\sigma$. It is normal force ($P$) per unit cross-sectional area (A).
$$ \sigma=\frac{P}{A} $$
Normal stress is caused by deformation due to axial forces and bending moments.
Shear stress
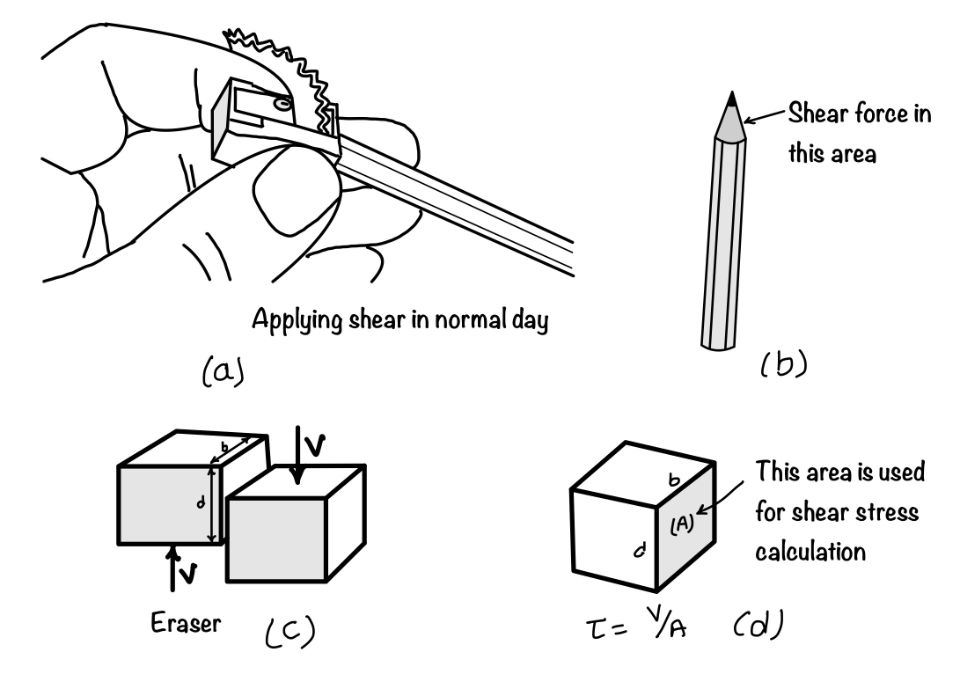
When we try to shear that eraser, as shown in the figure, the stress generated is the shear stress. You may find the shear stress parallel to the cross-sectional area. We represent the shear stress by the Greek letter gamma ($\tau$). And we define the shear stress as shear force ($V$) per unit cross-sectional area ($A$).
$$ \tau=\frac{V}{A} $$
Shear stress is caused by shear forces or Torsional moments.
Rectangular stress components
The state of stress at a point in 3D could be determined based on the six rectangular stress components.
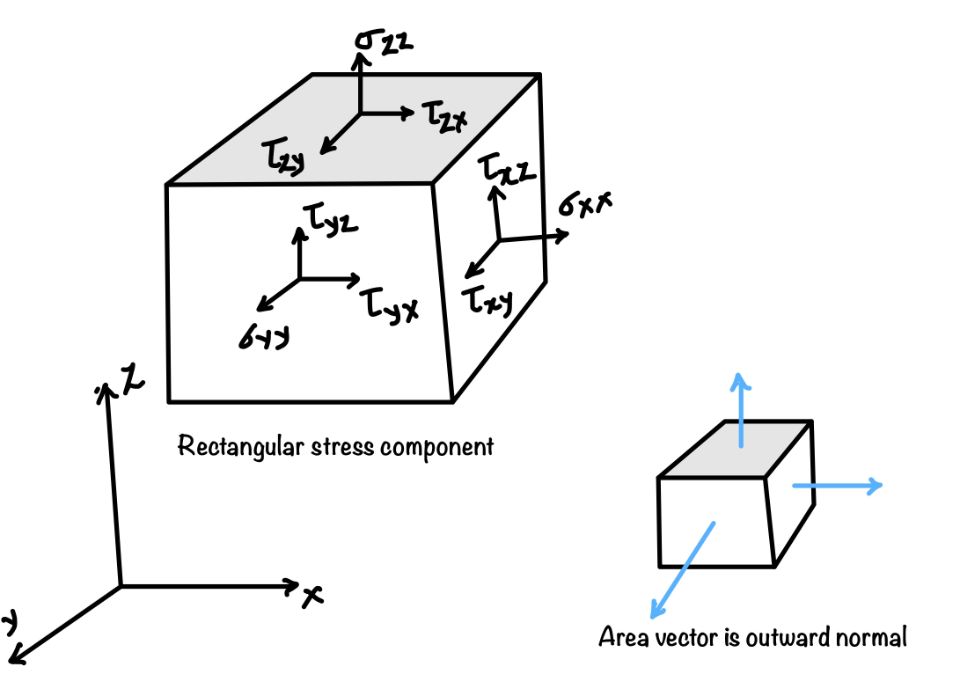
$$ \sigma= \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{bmatrix} $$
In this designation, the first subscript tells us the direction of the normal, and the second subscript tells us the direction of the stress component. This normal is perpendicular to the plane on which stress is acting. From the high school physic, we can remember the direction of the area is defined by its normal.
$\sigma_{xz}$ – Stress on $x$ plane in $z$ direction.
Stress component on an arbitrary plane
In this previous section, you learned two stress components, normal stress, and shear stress. Now If you want to find the normal and shear stress components on an arbitrary plane.
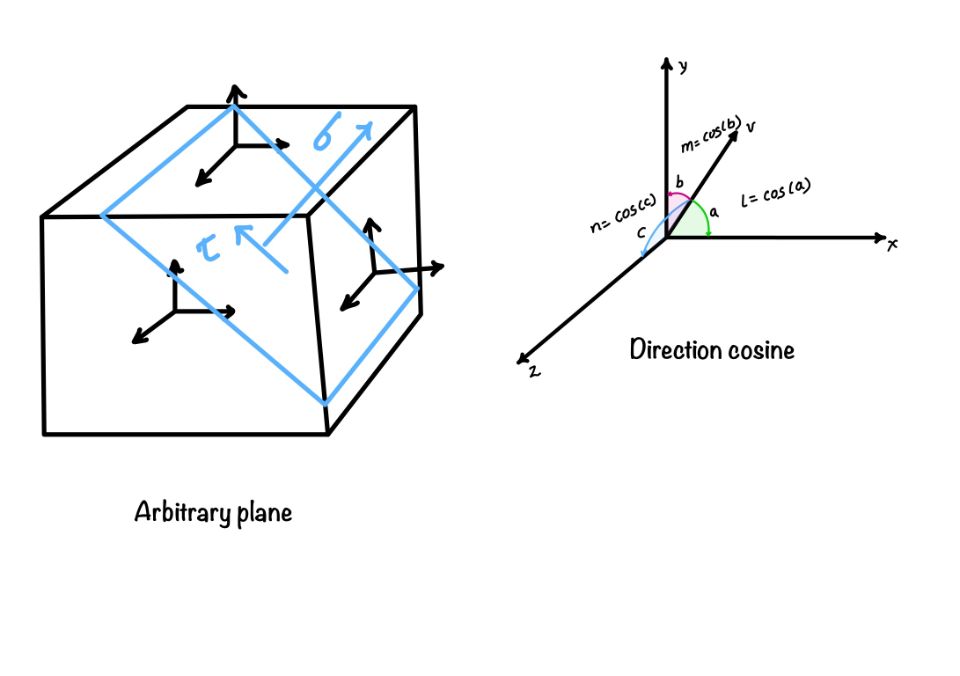
Suppose this plane has the direction cosines ($l, m, n$). Direction cosine is a way to describe the direction of a vector in space using the angles it makes with the x, y, and z axes. It helps us to break down the vector into its components in each direction.
You can find the stress from the following equations.
Let $S$ be the resultant stress vector on the plane. We can resolve them into components $S_x$, $S_y$, $S_z$ parallel to the three axis $x$, $y$, $z$. Thus
$$ S^2=S_x^2+S_y^2+S_z^2 $$
We can determine the stress components $S_x$, $S_y$ and $S_z$ from the following equation
$$ S= \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz}\\ \tau_{yx} & \sigma_{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \end{bmatrix}* \bigg\{\begin{matrix} l \\m\\n\end{matrix}\bigg\} $$
also, if $\sigma$ and $\tau$ are the normal and shear stress on the plane, then
$$ S^2=\sigma^2+\tau^2\\ \sigma=l.S_x+m.S_y+n.S_z\\\tau^2=S^2-\sigma^2 $$
What is Principal stress?
You have seen that stress at the point has different values for a different plane. Hence, for a given state of stress at a point $P$, we could determine the state of stress along any direction cosines $\{l m n\}$ by the use of formulas described in the previous section.
Suppose the normal stress calculated in a particular direction is an extremum (i. e. it has the highest or the lowest possible value). In that case, the stress is termed principal stress, and the direction described by the direction cosines is the principal stress direction associated with $\sigma$.
The principal stress could be determined by solving the cubic equation:
$$ \sigma^3-I_1\sigma^2 +I_2\sigma-I_3=0\\I_1=\sigma_{xx}+\sigma_{yy}+\sigma_{zz}\\I_2=\sigma_{xx}\sigma_{yy}+\sigma_{yy}\sigma_{zz}+\sigma_{zz}\sigma_{xx}-\sigma_{xy}^2-\sigma_{yz}^2-\sigma_{zx}^2\\I_3=\det (\sigma) $$
Where $I_1$, $I_2$, and $I_3$ are called the first, second, and third invariants of stress. In mathematics and physics, an invariant is a property of an object or a system that remains unchanged under a particular transformation or operation.
You can obtain the principle direction associated with $\sigma_1$, $\sigma_2$ and $\sigma_3$ by substituting $\sigma_i (i=1,2,3)$ in the following equation and solving for $l$, $m$, $n$.
$$ (\sigma_{xx}-\sigma_i)l+\sigma_{xy}m+\sigma_{xz}n=0\\\sigma_{xy}l+(\sigma_{yy}-\sigma_i)m+\sigma_{yz}n=0\\l^2+m^2+n^2=0 $$
What is the significance of octahedral stress?
Let’s discuss the importance of octahedral stress. Octahedral stress is an important parameter in the study of material behavior under complex loading conditions, as it provides a single scalar value that represents the overall level of stress in the material.
Now you must be thinking why we call it octahedral stress. To answer this, we would like to introduce the plane on which octahedral stress is acting. It acts on a plane that is equally inclined to all three principal axes. And you can have eight such planes. This is why we call it the octahedral plane. And the stress acting on the octahedral plane is octahedral stress.
Now let’s do some math here. We want to find the direction cosine of the octahedral plane.
$$ l=m=n=\pm \frac{{1}}{\sqrt3} $$
After defining the plane, it’s time to define the normal and shear stress components in these planes.
- Octahedral normal stress: $\sigma_{oct} = \frac{1}{3}(\sigma_1+\sigma_2+\sigma_3)$
- Octahedral shear stress: $\tau_{oct}=\frac{1}{3}\sqrt{(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2}$
What is volumetric and deviatoric stress?
Volumetric stress, also known as hydrostatic stress, is a measure of the uniform or isotropic compression or expansion of a material. It is equal to one-third of the trace of the stress tensor and does not depend on the orientation of the coordinate system. Volumetric stress is important in the study of materials that experience uniform pressure, such as fluids or gases.
Deviatoric stress, on the other hand, is a measure of the shear stress on a material, which causes deformation without changing the material’s volume. You can calculate it as the difference between the stress tensor and the volumetric stress, and it does depend on the orientation of the coordinate system. Deviatoric stress is important in the study of materials that experience non-uniform or directional stress, such as solids undergoing bending or torsion.
Together, volumetric stress and deviatoric stress provide a complete description of the stress state in a material, allowing researchers and engineers to understand and predict the material’s behavior under different loading conditions.
We can express the stress tensor ($S$) as the sum of two other tensors.
A volumetric stress tensor is related to the volume change of the body.
Deviatoric stress tensor, which is related to the distortion of the body.
$$ \sigma= \begin{bmatrix} \sigma_{m} & 0 & 0\\ 0 & \sigma_{m} &0\\ 0 & 0 & \sigma_{m} \end{bmatrix} $$
$$ \sigma= \begin{bmatrix} \sigma_{xx}-\sigma_m & \sigma_{xy} & \sigma_{xz}\\ \sigma_{yx} & \sigma_{yy}-\sigma_m & \sigma_{yz}\\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz}-\sigma_m \end{bmatrix} $$
Where:
$$ \sigma_m=\frac{\sigma_{xx}+\sigma_{yy}+\sigma_{zz}}{3} $$
Conclusion
Stress is a very important concept in solid mechanics. However, in the initial days of learning, it also needs to be clarified. This article explains the stress concepts in depth and clears every possible misconception. But still, if you have some doubts, please write us. After stress, we will explain the strain at a point.
In this article, you have learned the following key points:
- Stress: It is the intensity of internal forces at a point.
- Normal stress: It is a component of stress which is acting perpendicular to the cross-section.
- Shear stress: It is a component of stress which is acting parallel to the cross-section.
- Principal stress: It is the maximum or minimum normal stress value of stress at a point.
- Principal Plane: It is the plane on which the principal stress is acting.
- Octahedral stress: It is the stress which is acting on the octahedral plane. It is useful in understanding the material behavior in a single scalar value.
- Volumetric stress: We often call it hydrostatic stress. It measures the volumetric deformation of the material. You can define it as one-third of the trace of stress components.
- Deviatoric stress: It is a measure of shear stress in the material. It causes deformation without causing volume change.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


