Find a pen or pencil on your table hold one end tightly and rotate with the other end. The pen or pencil in your hand is subjected to torque. This torque will create torsion in the pen.
In this article, we will learn about the members subjected to torsion. We will also learn how these members are resisting the torsion. What is the torsion formula? What is the practical use of the torsion formula?
Relation between shear strain and shear stress
In this section we will derive the relation between shear strain and the shear stress in the circular shaft. For this we will first define the shear strain in the circular shaft as shown in the figure.
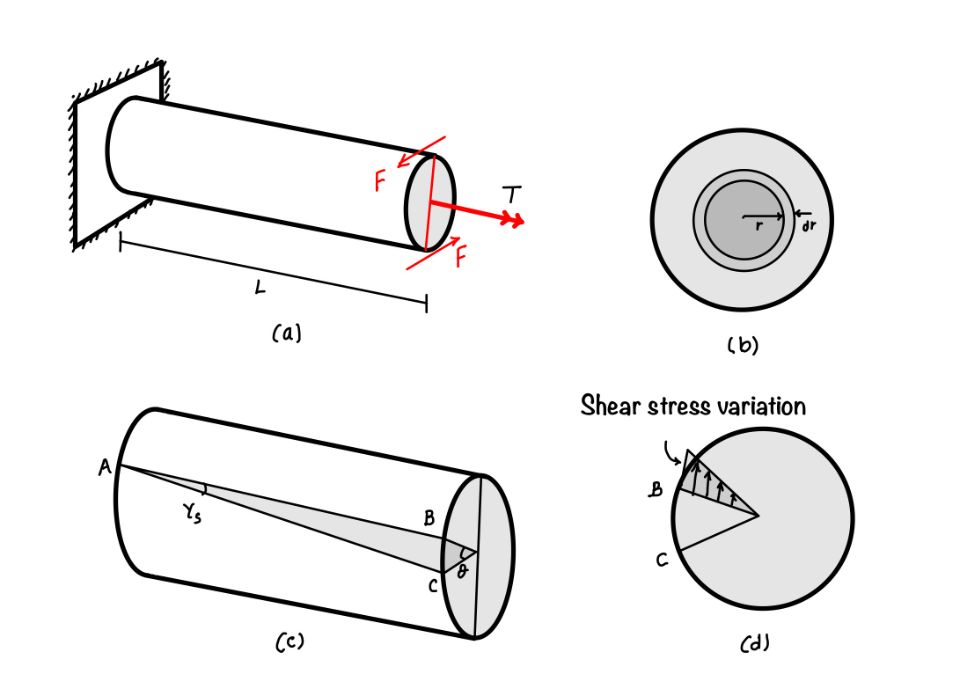
When you see the part C of the figure you can write the shear strain in the shaft as follows:
$$ \gamma_s = \frac{BC}{L} $$
Angle of twist $\theta$ can be defined as :
$$ \theta = \frac{BC}{R} $$
$$\Rightarrow BC = R\theta$$
Now from the above equation we can write the shear strain $\gamma$ as:
$$ \gamma_s = \frac{R \theta}{L} $$
Hence the for shear strain at any location $r$ , we can write as:
$$\gamma = \frac{r\theta}{L} $$
Shear stress and shear strain are related with the shear modulus of elasticity or modulus of rigidity.
$$ \tau = \gamma G = \frac{r\theta G}{L} $$
The above equation shows that the shear stress varies with the radius $r$. This is the linear relation and hence you can see the shear stress variation in part (d) of the figure.
Relation between shear stress and torque
In this section we will establish the relation between the shear stress and applied torque. When we will integrate the shear stress over the strip of circular disc as shown in part (d) of the figure we will get the torsion.
Shear force in the elementary area
$$ \text{Shear force} = \tau \times \underbrace{(2\pi r \times dr)}_{\text{Area}} $$
Torque due to shear force on the the elementary area
$$=\tau\times (2\pi r\times dr)\times r$$
Hence from here we can find the external torque $T$ must be equal to the torque due to internal forces. To find this we need to integrate over the entire cross-section
$$ T= \int_0^R {\tau\times (2\pi r\times dr)\times r} \Rightarrow \int_0^R\frac{r\theta G}{L}(2\pi r dr)r $$
$$T =\frac{\pi R^4}{2}\times \frac{\theta G}{L} \Rightarrow T=\frac{JG\theta}{L} $$
From here we can find the pure torsion formula as:
$$\frac{T}{J}=\frac{\tau}{r}=\frac{G
\theta}{L} $$
Limitations
Limitation of the formula discussed above:
- Warping: Plane section remains plane after torsion and there is no warping.
- Rotation: All cross-sections normal to longitudinal axis at equal distance undergo dame relative rotation.
- Homogenous and Isotropic: We considered the material is homogenous and isotropic.
Application
We use the pure torsion formula to calculate a shaft’s power transfer capacity but keep in mind that this equation is applicable exclusively to circular shafts.
Conclusion
In this article we have discussed the pure torsion formula. The shafts are mainly subjected to the torsion.
In this article you have learned following points:
- Torsional Stress Derivation: Understanding stress in circular shafts due to torsion involves a detailed derivation, revealing the intricacies of the phenomenon.
- Shear Strain and Shear Stress Relationship: The article establishes a clear connection between shear strain and shear stress, elucidating their dependence on the shear modulus of elasticity.
- Derivation of Pure Torsion Formula: Investigating the relationship between shear stress and applied torque. Culminating in the derivation of the pure torsion formula for circular shafts.
- Limitations of the Formula: Recognizing the need to understand the formula’s boundaries. Outlining considerations for warping, rotation, and material homogeneity. Providing a realistic view of the formula’s applicability.
- Practical Application in Power Transmission: The pure torsion formula finds practical utility in determining the capacity of circular shafts to transmit power.
- Formula Applicability Reminder: It is important that we derive the pure torsion formula specifically for circular shafts, limiting its application to this particular geometry.
- Conclusion on Significance: The article concludes by highlighting the importance of the pure torsion formula in comprehending and analyzing the behavior of circular shafts under torsional loads.
Solid Mechanics
In this app, you would be able to explore the world of Solid Mechanics. The app covers many important topics in the field of solid mechanics.
- Interactive Mohr’s Circle of Stress and Strain.
- Calculators for Stress and Strain Analysis.
- Graphical representations of failure criteria.
- A detailed description of key concepts of Solid Mechanics with diagrams.
This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are:
Author


