In the previous articles, we have seen simple steps to calculate the tensile strength of flat plates for simple and staggered bolting using IS 800:2007. In this article, let’s explore the steps for determining the tensile strength of angle sections when bolted to a gusset plate.

Are design equations of angle sections different from that of flat plates? Answer: Yes

As previously discussed in the article, a tension member can fail in primarily three modes:

a) Design strength due to yielding of the gross section$(T_{dg})$

b) Design strength due to rupture of critical section $(T_{dn})$

c) Design strength due to block shear $(T_{db})$

Clause 6.3.1 IS 800:2007 provides design specifications to determine $T_{dn}$ for flat plates i.e.,

$$ T_{dn}=0.9A_nf_u/\gamma_{m1} $$

Whereas, for angle sections connected to one leg as per clause 6.3.3 IS 800:2007

$$ T_{dn}=0.9A_{nc}f_u/\gamma_{m1}+\beta A_{go}f_y/\gamma_{m0} $$

Now the question arises, what is the difference? What is $\beta$? The answer is the shear lag effect. Follow the article till the end to know about it.

Shear lag effect in angle sections

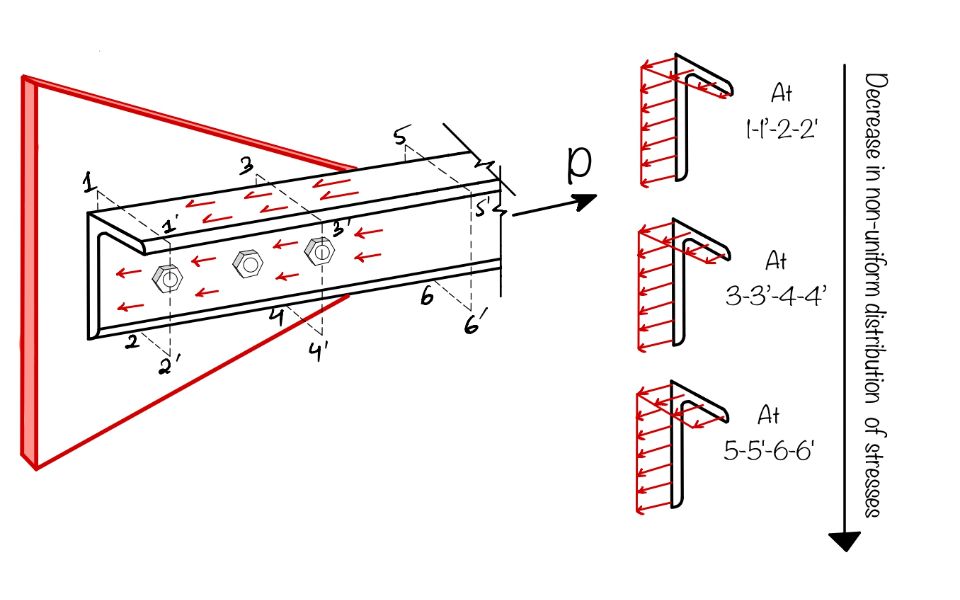
The figure above shows a single-angle section connected through one leg to a gusset plate.

It can be seen from the figure that for a section away from the end connection (Section 5-5’-6-6’), the tensile stress distribution is uniform. Whereas, the tensile stress distribution at the critical section (the section where net effective area of cross-section is minimum, Section 1-1’-2-2’) will be non-uniform.

It is so because the distribution of stresses in the outstanding/unconnected leg takes place through shear forces.

In such a case, the connected leg will have higher tensile stresses(in the order of ultimate stresses) whereas the outstanding leg will be comparatively lesser (in the order of yield stresses)

Because the internal transfer of forces from the connected leg to the outstanding leg happens by shear and the outstanding leg ‘lags’ behind the connected leg in contribution to resist the tensile load, the phenomenon is called “Shear lag”.

IS 800:2007 provisions for shear lag effect

As per clause 6.3.3 IS 800 :2007, for single angle sections,

$$ T_{dn}=0.9A_{nc}f_u/\gamma_{m1}+\beta A_{go}f_y/\gamma_{m0} $$

where,

$\beta=$ $1.4-0.076(w/t)(f_y/f_u)(b_s/L_c)\leq(f_u\gamma_{m0}/f_y\gamma_{m1})\geq 0.7$

$w=$ outstand leg width;

$b_s=$ shear lag width as shown in figure below;

$L_c=$ Length of end connection as shown in figure below;

$A_{nc} =$ Net area of the connected leg;

$A_{go} =$ Gross area of the outstanding leg;

$t=$ Thickness of the leg

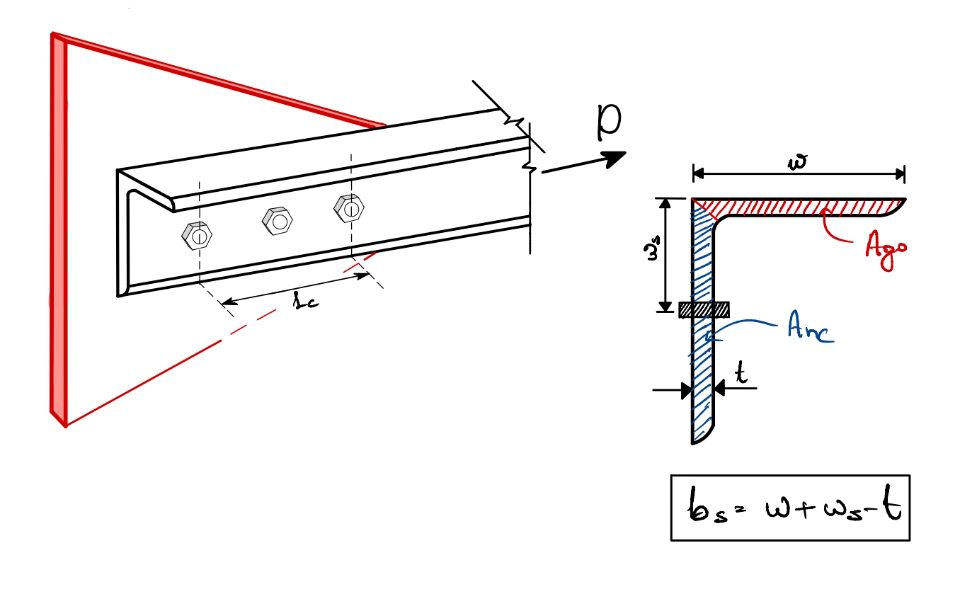
Here, the $\beta$ factor is used for quantification of non-uniformity of stress distribution.

Design example

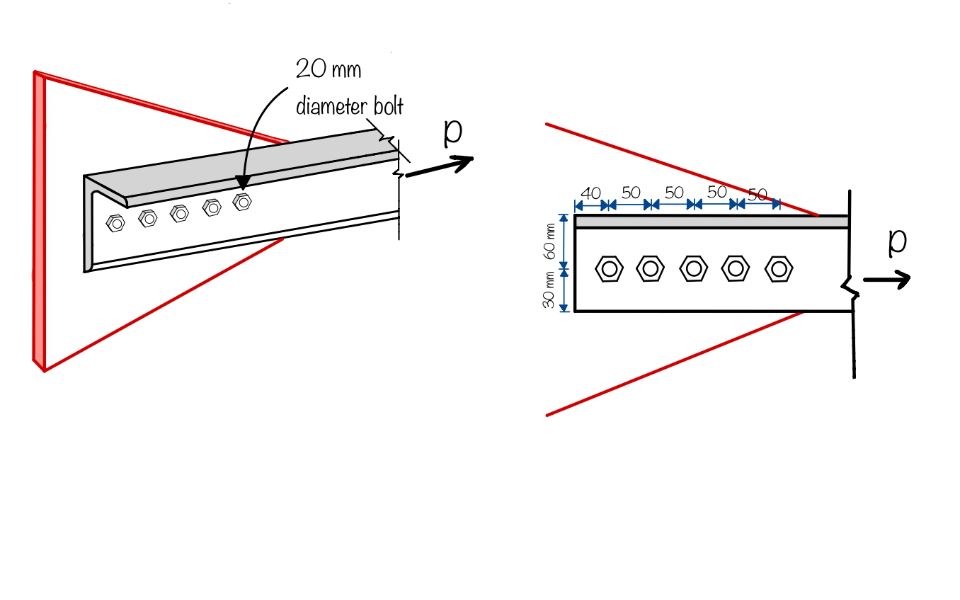
Determine the tensile capacity for the section ISA 90 $\times$ 60 $\times$ 8 shown below.

Given,

$f_y=250\; MPa$

$f_u=410\; MPa$

Using SP 6:Part 1, for ISA 90 $\times$ 60 $\times$ 8

$A_g=1137\;mm^2$

Now, design tensile strength, $T_d=\text{Min} (T_{dg},\,T_{dn},\,T_{db})$

For $T_{dg }$

Using Clause 6.2 IS 800 :2007,

$$ T_{dg}=A_gf_y/\gamma_{m0} $$

Hence,

$$ T_{dg}=1137\times250/1.10= 258.41\; kN $$

For $T_{dn }$

For single-angle, as per IS 800 :2007

$$ T_{dn}=0.9A_{nc}f_u/\gamma_{m1}+\beta A_{go}f_y/\gamma_{m0} $$

where,

$\beta=$ $1.4-0.076(w/t)(f_y/f_u)(b_s/L_c)\leq(f_u\gamma_{m0}/f_y\gamma_{m1})\geq 0.7$

In the given problem,

$w=60\; mm$; $t=8\; mm$;

$b_s=w+w_1-t=60+60-8=112\; mm$

$L_c =200 \; mm$

Hence,

$\beta=$ $1.4- 0.076 (60/8) (250/410) (112/200) =1.205$

$(f_u\gamma_{m0}/f_y\gamma_{m1})=(410\times1.10)/(250\times 1.25)=1.443\geq0.7$

Hence, $\beta=1.205$

Now,

$A_{go}=(60-8/2)\times8=448\; mm^2$

$A_{nc}=(90-8/2-20)\times 8=528\; mm^2$

Hence,

$$ T_{dn}=0.9A_{nc}f_u/\gamma_{m1}+\beta A_{go}f_y/\gamma_{m0} $$

$$ T_{dn}=0.9\times 528\times 410/1.25+1.205\times 448 \times 250/1.10=278.56\; kN $$

For $T_{db }$

$$ T_{db}=Min(T_{db_1},T_{db_2}) $$

Which can be calculated with the two cases shown below,

$$ T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}} $$

$$ T_{db_2}=\frac{0.9A_{vn}f_u}{\sqrt{3}\gamma_{m1}}+\frac{A_{tg}f_y}{\gamma_{m0}} $$

Now,

$A_{vg }=240 \times 8= 1920\;mm^2$

$A_{vn}= [240 – (4.5\times 20)]\times 8 = 1200\; mm^2$

$A_{tg }= 30\times 8 = 240 \; mm^2$

$A_{tn }=(30 – 0.5\times 20) \times 8 = 160 \; mm^2$

Hence,

$$ T_{db_1}=\frac{A_{vg}f_y}{\sqrt{3}\gamma_{m0}}+\frac{0.9A_{tn}f_u}{\gamma_{m1}} $$

and now put the values

$$ T_{db_1}=\frac{1920\times250}{\sqrt{3}\times1.10}+\frac{0.9\times160\times410}{1.25}= 299.17\; kN $$

$$ T_{db_2}=\frac{0.9A_{vn}f_u}{\sqrt{3}\gamma_{m1}}+\frac{A_{tg}f_y}{\gamma_{m0}} $$

Now put the values in formula

$$ T_{db_2}=\frac{0.9\times1040\times410}{\sqrt{3}\times1.25}+\frac{240\times250}{1.10}=231.80\; kN $$

Hence, $T_{db}=231.80\; kN$

Thus, design tensile strength, $T_d=\text{Min} (T_{dg},\,T_{dn},\,T_{db})$

$=(258.41\; kN, 278.56\; kN, 231.80\; kN) = 231.80 \; kN$

Conclusions

In this article we discussed:

i) Shear lag effect exists when the load transfer takes place through only one connected leg.

ii) The calculation steps involving shear lag is explained.

Android Apps

⭐️ ⭐️ ⭐️ ⭐️ ⭐️ 1000+ | 400,000 + Downloads (Cumulative)

At eigenplus, our goal is to teach civil engineering students about structural analysis and design starting from the fundamental principles. We do this with the help of interactive android applications and accompanying web articles and videos.

Our apps have helped more than 400 thousand students across the world to understand and learn the concepts of structural engineering. Check out our apps on the google play store.

KNOW MORE

This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are: