A polytropic process is a thermodynamic process in which a polytropic equation is used to describe the relationship between pressure and volume. These processes are frequently used to simulate compressors and expanders in real-world engineering applications, such as air conditioning systems, refrigeration systems, and gas pipelines.

Understanding how polytropic processes work and how to apply them can help to improve the efficiency of a wide range of engineering systems and technologies.

Definition of Polytropic process

A polytropic process is a thermodynamic process in which the pressure and volume of a gas or fluid change in a way that is described by the polytropic equation. Mathematically, the polytropic equation is defined as:

$$PV^n = C$$

, where P is pressure, V is volume, n is the polytropic index, and C is a constant. The polytropic index, n, is a dimensionless number that describes the relationship between pressure and volume for a particular system.

Graphically, this process can be represented as

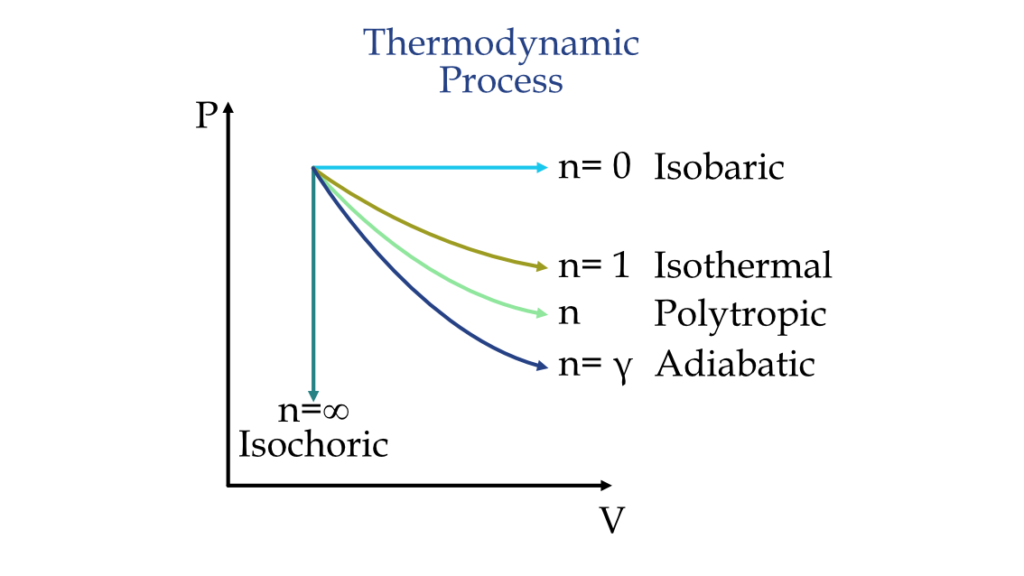
When n = 1, the process is isothermal, when n = 0, it becomes an isochoric process, when n = $\infty$, it becomes isobaric, and when n = γ, it becomes adiabatic. where γ = Cp/Cv is the heat capacity ratio.

For a polytropic process, the work done by the gas or fluid, W, can be calculated using the equation

$$\mathrm{W}=\frac{P_1 V_1-P_2 V_2}{n-1}$$

where V_1 and V_2 are the initial and final volumes of the gas or fluid.

This formula is applicable to ideal gas or fluid, and the real gas or fluid has to use the real equation of state, like the Van der Waals equation or Redlich-Kwong equation, to consider the deviation from the ideal gas behavior.

Derivation of work done

To derive the expression for work done in a polytropic process, let’s consider a system undergoing compression or expansion. This process can be represented mathematically using the following equation:

$$P * V^n = Constant$$,

where P represents the pressure, V denotes the volume, and n is the polytropic index. The polytropic index, which can be positive, negative, or zero, is a measure of the relationship between pressure and volume during the process.

The work done on the system during the polytropic process can be determined by integrating the pressure-volume relationship over the defined limits. Using the equation above, we express the work done (W) as follows:

$$W = ∫ P dV$$

To proceed with the integration, we need to express pressure (P) in terms of volume (V). By rearranging the polytropic equation, we obtain:

$$P = C/ V^n$$

Substituting this expression into the equation for work done, we have:

$$W = ∫ (C/ V^n) dV$$

This becomes

$$ \mathrm{W}=\left[\frac{C \cdot V^{1-n}}{1-n}\right]_1^2$$

$$\mathrm{W}=\frac{C . V_2^{1-n}}{1-n}-\frac{C . V_1^{1-n}}{1-n}$$

On rearranging the term, we get

$$\mathrm{W}=\frac{P_1 V_1-P_2 V_2}{n-1}$$

Here n is the polytropic index, $P_1$, $V_1$ and $P_2$, $V_2$ are initial and final pressure and volume respectively.

This is the formula for the work done during this process in a closed system.

Conclusions

The polytropic process is a useful concept in engineering as it allows for the efficient compression and expansion of gases in various systems and devices. The polytropic exponent, which is a measure of the efficiency of this process, can be used to optimize the performance of these systems and devices.

Key Learning Points:

Definition: A polytropic process is a thermodynamic transformation characterized by a relationship between pressure and volume, expressed as $P * V^n = \text{Constant}$, where n is the polytropic index.
Work done: The work done in this process is $\mathrm{W}=\frac{P_1 V_1-P_2 V_2}{n-1}$.
Applications: These processes are commonly found in Compressors, Turbines, Nozzles, Porous media, Pipes, and diffusers
Polytropic index: The polytropic index or exponent, a measure of the efficiency of this process, which can be used to optimize the performance of these systems.

This article was crafted by a group of experts at eigenplus to ensure it adheres to our strict quality standards. The individuals who contributed to this article are: